|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこのグラフ図を利用してください.
応用分野:
テイラーの定理,
ロルの定理
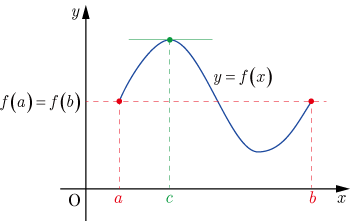
関数が閉区間 で連続,開区間 で微分可能で, であるとき, となる が少なくとも1つ存在する.
■証明
I. が定数関数の場合
が定数関数の場合,すなわち, ( は定数)なら,開区間 で常に となり主張は成り立つ.
II.I 以外の場合
I 以外の場合なら,開区間 で が最大値 ( , ),あるいは,最小値 ( , )をとる が存在する.
(i) で最大値をとる場合
で最大値をとる場合, の正負に関わらず
となる.
よって, なら
したがって,
・・・・・(1)
となりる.
なら
したがって,
・・・・・(2)
となる.
関数 が閉区間で連続,開区間で微分可能であるので が存在し
・・・・・(3)
が成り立つ.
(1),(2),(3)より
となる.
(ii) で最小値をとる場合
で最小値をとる場合, の正負に関わらず
となる.よって, なら
したがって,
・・・・・(4)
となり, なら
となる.したがって,
・・・・・(5)
となる.
関数 閉区間 で連続,開区間 で微分可能であるので が存在し
・・・・・(6)
が成り立つ.
(4),(5),(6)より
となる.
以上より,定理が成り立つ.
【参考図書】
・基礎課程 解析学 編者:水野克比古 出版社:株式会社学術図書出版
・Calculus 7E 著者:James Stewart 出版社:Brooks/Cole Pub Co
最終更新日: 2023年5月29日