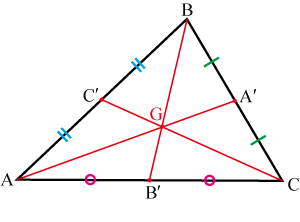
まず
△
の面積を
,△の面積を
,
△の面積を
,△の面積を
,
△の面積を
,△の面積を
,
とする.
,, は各辺の中点であるから
・・・・・・(1)
・・・・・・(2)
・・・・・・(3)
△面積(
)
△の面積() ・・・・・・(4)
△の面積()
△の面積()
・・・・・・(5)
△の面積()
△の面積()
・・・・・・(6)
(1),(4)より
・・・・・・(7)
(1),(2),(7)より
・・・・・・(8)
(2),(5)より
・・・・・(9)
(1),(3),(9)より
・・・・・・(10)
(8),(10)より
・・・・・・(11)
したがって
△の面積(
):△の面積(
)
以上より
同様にして
同様にして
【証明終了】(クリックで閉じる)