2点間の距離
点Pと点Qの2点間の距離,言い換えると線分PQの長さを,2点の座標成分を使って表現する方法を,
について述べる.
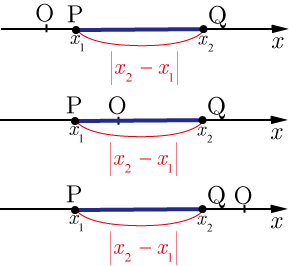 ■数直線の場合 ■数直線の場合
軸上に点Pと点Qがあり,その座標成分をそれぞれ
,とする.ただし,
である.
この場合,線分OPの長さは
,線分
OQの長さは
である.
●
かつの場合
線分OPの長さは,線分OQの長さから線分OPの長さを差し引いたものとなる.すなわち,
・・・・・・(1)
となる.
●
かつ
の場合
線分OPの長さは,線分OQの長に線分OPの長さ加えたものとなる.すなわち,
・・・・・・(2)
となる.
●
かつ
の場合
線分OPの長さは,線分OQの長さから線分OPの長さを差し引いたものとなる.すなわち,
・・・・・・(3)
となる.
(1),(2),(3)は絶対値を使うと,
となる.また,
であるので,結局2点間の距離は,ただ単に2点の座標成分の差の絶対値になる.この時,座標成分の大小を考えなくてもよい.
PQは直角三角形PQAの斜辺になる.三平方の定理より,
となり,よって
となる.
PQは直角三角形PQBの斜辺になる.三平方の定理より,
となる.BPは直角三角形BAPの斜辺になる.三平方の定理より,
となる.したがって,
となる.
ホーム>>カテゴリー分類>>幾何>>2点間の距離
初版:2007年11月22日,最終更新日:
2015年4月7日
|