加法定理の証明
(複号同順)
■証明
一般的な証明を紹介する.(ベクトルを用いた証明,オイラーの公式を用いた導出もある.)
単位円上に点P,Qがある.OPと 軸のなす角を OQと 軸のなす角を とする.
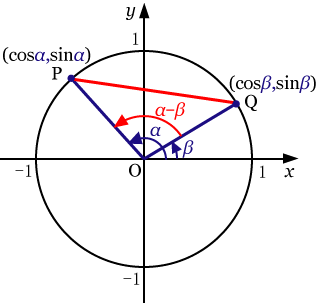 三角形OPQを考える.余弦定理より,
三角形OPQを考える.余弦定理より,
・・・・・・(1)
線分PQの長さを点P,点Qの座標成分を用いて表すと,
・・・・・・(2)
(1),(2)より,
よって,
- ・・・・・・(3)
(3)を用いて他の加法定理の公式も導くことができる.以下にそれを示す.
((3)より)
・・・・・・(4)
・・・・・・(5)
・・・・・・(6)
分子,分母を
で割ると,
・・・・・・(7)
分子,分母を
で割ると,
・・・・・・(8)
ホーム>>カテゴリー分類>>三角関数>>加法定理>>加法定理の証明
最終更新日
2023年3月2日
 三角形OPQを考える.余弦定理より,
三角形OPQを考える.余弦定理より,