|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこのグラフ図を利用してください.
応用分野:
2重根号のはずし方,
累乗根の証明(累乗根の積),
累乗根の証明(累乗根の商),
累乗根の証明(累乗根の累乗),
累乗根の証明(累乗根の累乗根),
累乗根の証明(累乗の累乗根),
続きを見る
問題リスト←このページに関連している問題です
累乗根
を正の整数とするとき,数を乗するとになる数のことを の 乗根といい,式で書くと
( :正の整数)
の関係がある.
の関係を用いて乗根を考える.
■ が奇数の場合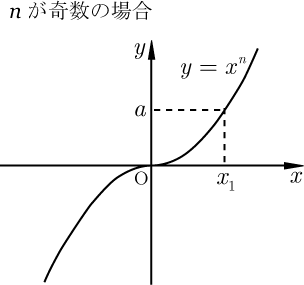
のとき, を満たす はただ1つ定まる.その値 が の 乗根で
と表す.
図からわかるように
ならば,
ならば,
となる.
■ が偶数の場合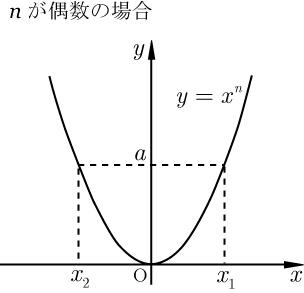
のとき, を満たす は2つ定まる.
正の方 を
負の方 を
と表す.
必ず となることに注意する. 例としては, ではなく である.
また
のとき,
とし
のとき, を満たす は存在しない
とする.
2乗根を平方根,3乗根を立方根ともいう.2乗根は とは書かず2を省略して と書く.
の 乗根 を 乗すると となる.すなわち
累乗根の計算は,以下に示す計算法則が成り立つ
最終更新日: 2023年7月28日