|
|||||||||||||
|
|||||||||||||
|
関連するページを見るにはこのグラフ図を利用してください.
問題リスト←このページに関連している問題です
指数関数
, とするとき, の関数を を底とする指数関数という.
(任意の に対して の値が定まるので, は の関数である)
■関連動画
■指数関数の性質
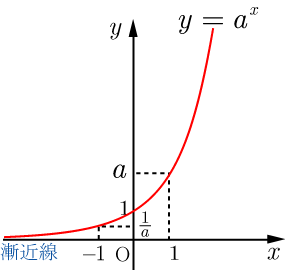
● の場合 ⇒詳細
の値が増加すれば, の値も増加する 単調増加である(単調増加関数).
すなわち,
(大小関係はかわらない)
の値が減少すると,グラフは 軸に限りなく近づく( 軸が漸近線)
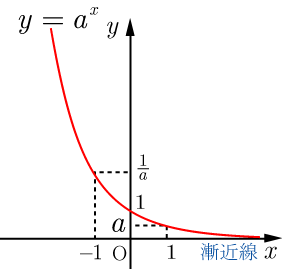
● の場合 ⇒詳細
の値が増加すれば, の値は減少する 単調減少である(単調減少関数).
すなわち,
(大小関係は逆になる)
の値が増加すると,グラフは 軸に限りなく近づく( 軸が漸近線)
●共通する特徴
定義域:実数全体 , 値域:正の数全体
グラフは点 を通る.
( は単調増加あるいは単調減少するので, と は1対1の関係であることによる. )
と すなわち, と は 軸に対して対称である.
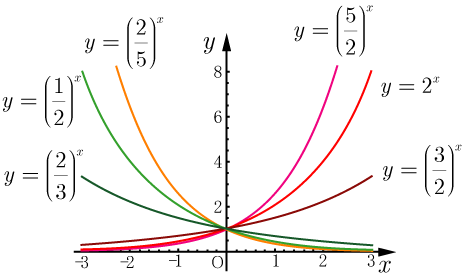
具体的な指数関数のグラフを示す.
最終更新日: 2024年2月22日