単振り子 : 周期の厳密解の導出 (derivation of excact solution of period)
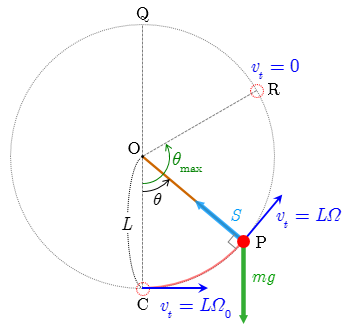
図のような,半径
L
の円弧上を質量
m
の質点が運動する単振り子について,最下点 C を重力による位置エネルギーの基準にとったときの力学的エネルギー保存則
12
mvt2
+
mgL
(
1−cosθ
)
=
12
mv02
- - - (1)
を考える.ここで,
v0
は最下点 C における質点の速さである.質点が最高点 Q (
θ=π
) に達する場合,点 Q で運動エネルギーは 0 以上なので,式 (1) より
12
mv02
−2mgL≥0
- - - (2)
が成り立つ.この場合,点 Q での運動エネルギーが 0 なら質点は点 Q で静止し,0 より大きければ一方向に回る回転運動をする.質点が最高点 Q に達しない場合
12
mv02
−2mgL<0
- - - (3)
が成り立ち,質点は
−θmax
≤θ≤
θmax
の範囲で往復運動をする.ここで,角
θmax
(<π)
は
12
mv02
=
mgL
(1−cos
θmax
)
- - - (4)
を満たす.回転運動する場合は1回転にかかる時間を,往復運動する場合は1往復にかかる時間を,単振り子の周期とする.最高点 Q で静止する場合は周期を定義できない.
角速度
Ω=
dθdt
を用いて,速度の接線方向成分を
vt=
Ldθdt
=LΩ
と表し,最下点 C での角速度の大きさを
Ω0
とすると
v0
=LΩ0
である.これらの表記で式 (1) を整理すると
Ω2
=
Ω02
−2gL
(
1−cosθ
)
- - - (5)
となる.したがって,
Ω=
dθ
dt
=
±
Ω02
−
2gL
(
1−cosθ
)
=
±2
gL
Ω02L
4g
−
1−cosθ
2
=
±2
gL
k2
−
sin2
θ2
- - - (6)
を得る.ここで
k=
Ω02
Lg
を用いた.
θ=π
のとき,式 (6) の右辺のルート中の式は
k2−1
となり,
k≥1
であれば,最高点 Q で角速度
|Ω|≥0
なので,式 (2) の状況(最高点 Q で静止,もしくは回転運動)に対応する.
k<1
であれば式 (3) の状況(往復運動)に対応する.式 (6) を変数分離すると形式的に
dt
=
±12
Lg
dθ
k2
−
sin2
θ2
- - - (7)
と表せる.式 (7) について,
k<1
(往復運動)
,
k>1
(回転運動)
,
k=1
(最高点で静止)
の3つの場合に分けて考え,往復運動・回転運動の場合はその周期を導出する.
◆
k<1
(往復運動)の場合
この場合,角速度
Ω=0
となるような角
θmax
(<π)
が存在し,式 (6) より
k=sin
θmax
2
- - - (8)
を満たす(式 (4) に対応している).時刻
t=0
において
θ=0
,
Ω=
Ω
0
とすると,
t=0
から質点が最初に角
θ=
θmax
に達するまでの時間が周期
T
の4分の1である.この間は
Ω>0
であるので,範囲
0≤θ≤
θ
max
において,式 (7) を積分すると
t
=
12
Lg
∫0θ
dθ
k2
−
sin2
θ2
- - - (9)
が得られる.ここで,
sinθ2
=kz
とおくと
dz
dθ
=
12k
cosθ2
=
12k
1−
sin2
θ2
=
12k
1−k2
z2
なので,置換積分を行うと式 (9) は
t=
12
Lg
∫0
z=1k
sinθ2
1
k2−
k2z2
2k
1−k2
z2
dz
=Lg
∫0z
dz
(
1−
z2
)(1−
k2z2
)
- - - (10)
となり,第1種の楕円積分の標準形で表される.さらに,
z=sinφ
とおくと
dz=cosφdφ
より
t=
Lg
∫0
φ=
sin−1z
cosφdφ
(1−
sin2
φ)(1−
k2sin2
φ)
=
L
g
∫0φ
dφ
1−
k
2
sin
2
φ
- - - (11)
となる.式 (10) もしくは式 (11) において,角
θ=
θmax
に達するまでの時間(周期
T
の4分の1)を考えると,式 (8) より
z=
1k
sin
θmax
2
=1
,および
φ=
sin−11
=π/2
より
T4
=
Lg
∫01
dz
(
1−z2
)
(
1−k2
z2
)
=
Lg
∫0
π/2
dφ
1−k2
sin2
φ
- - - (12)
が得られる.第1種の完全楕円積分
K(k)
=
∫01
dz
(
1−z2
)
(
1−k2
z2
)
=
∫0
π/2
dφ
1−k2
sin2
φ
- - - (13)
の表記を用いると,周期
T
は
T=4
Lg
K(k)
--- (14)
と表される.
Ω0
が非常に小さい微小振動(
k≪1
)の場合,式 (13) において
1−k2
sin2φ
≈1
と近似できるので,第1種の完全楕円積分の値は
K(k)
≈
∫0
π/2
dφ
=π2
となる.したがって,周期は
T≈4
L/g
⋅
π2
=2π
L/g
となり,近似解における周期と一致する.
k
は小さいが
K(k)
において無視できない場合,展開式
1
1−x
=
(1−x)
−12
=
1+
12x
+
12!
⋅
322
x2
+
13!
⋅
3⋅5
23
x3
+⋯
=
∑
n=0
∞
(
2n−1
)!!
(2n)
!!
xn
(
−1<x<1
)
および,ウォリスの公式
∫
0
π/2
sin2n
φ dφ
=
2n−1
2n
⋅
2n−3
2n−2
⋅
2n−5
2n−4
⋯×
π2
=
π2
(
2n−1
)!!
(2n)!!
を用いて,
K(k)
=
∫0π/2
∑
n=0
∞
(
2n−1
)!!
(2n)
!!
(
k2
sin2φ
)
n
dφ
=
∑
n=0
∞
(
2n−1
)!!
(2n)
!!
k2n
∫0π/2
sin2n
φ dφ
=
π2
∑
n=0
∞
{
(
2n−1
)!!
(
2n
)!!
}
2
k2n
と展開し,最初の数項をとればよい.したがって,式 (8) を用いて
T=4
Lg
⋅
π2
∑
n=0
∞
{
(
2n−1
)!!
(
2n
)!!
}
2
(
sin2
θmax
2
)
n
=2π
Lg
{
1+
(12)
2
sin2
θmax
2
+
(
1⋅3
2⋅4
)
2
(
sin2
θmax
2
)
2
+
(
1⋅3⋅5
2⋅4⋅6
)
2
(
sin2
θmax
2
)
3
+⋯
}
--- (15)
と表すことができる.
◆
k>1
(回転運動)の場合
この場合,式 (6) より角速度
Ω≠0
なので,一方向に回転する.時刻
t=0
において
θ=0
,
Ω=
Ω
0
とすると,常に
Ω>0
となる.往復運動の場合と同様に式 (7) を積分する際に,
θ/2
=φ
とおくと
t
=
12
Lg
∫0θ
dθ
k2
−
sin2
θ2
=
1k
Lg
∫0φ
dφ
1
−
1
k2
sin2φ
- - - (16)
が得られる.
θ=0
から
π
までにかかる時間が周期
T
の半分なので,式 (16) において
θ=0
から
π
まで,つまり,
φ=0
から
π/2
まで積分すると
T2
=
1k
Lg
∫0
π/2
dφ
1
−
1
k2
sin2φ
- - - (17)
となる.したがって,第1種の完全楕円積分の式 (13) の表記を用いると,周期は
T
=
2k
Lg
K
(
1/k
)
- - - (18)
と表される.
Ω0
が非常に大きく(
k≫1
),式 (17) において
1−
sin2φ
/k2
≈1
と近似できる場合,周期は
T≈
2k
Lg
⋅
π2
=
πk
Lg
=
2π
Ω0
(
∵k=
Ω0
2
Lg
)
と近似できる(一定の角速度
Ω0
で回転する等速円運動の周期と同じ).
1/k
は小さいが
K
(
1/k
)
において無視できない場合,
κ=1/k
とおいて,式 (15) と同様に展開すると
T=2κ
Lg
⋅
π2
∑
n=0
∞
{
(
2n−1
)!!
(
2n
)!!
}
2
κ2n
=π
Lg
{
κ+
(12)
2
κ3
+
(
1⋅3
2⋅4
)
2
κ5
+
(
1⋅3⋅5
2⋅4⋅6
)
2
κ7
+⋯
}
--- (19)
と表すことができる.
◆
k=1
(最高点で静止)の場合
時刻
t=0
において
θ=0
,
Ω=
Ω
0
とし,式 (7) に
k=1
を代入して積分すると
t
=
12
Lg
∫0θ
dθ
1−
sin2
θ2
=
12
Lg
∫0θ
dθ
cosθ2
=
12
Lg
∫0θ
cosθ2dθ
cos2θ2
=
12
Lg
∫0θ
cosθ2dθ
1−
sin2
θ2
となり,
x=sinθ2
とおいて置換積分を行うと,
dx=
12
cosθ2
dθ
より
t
=
12
Lg
∫0
x=sinθ2
2dx
1−
x2
=
12
Lg
∫0x
(
11−x
+
11+x
)
dx
=
12
Lg
log
1+x
1−x
=
12
Lg
log
1+sinθ2
1−sinθ2
が得られる.さらに,
sinθ2
=
−cos
(
θ2
+
π2
)
を用いて
t=
12
Lg
log
1−cos
θ+π2
1+cos
θ+π2
=
12
Lg
log
sin2
θ+π4
cos2
θ+π4
=
Lg
log tan
θ+π4
--- (20)
が得られる.上式が
θ=0
から
θ
までにかかる時間を表している.ここで,
θ→π
の極限を考えると,
lim
θ→π
tanθ+π4
=
lim
x→π/2
tanx
=∞
より
t→∞
となるので,質点が最高点 Q (
θ=π
) に達するには無限の時間がかかることになる.さらに,式 (20) から
tanθ+π4
=
e
gL
t
,
cotθ+π4
=
e
−gL
t
と表せること,および
tanx+cotx
=
sinx
cosx
+
cosx
sinx
=
sin2x
+
cos2x
sinxcosx
=
1sinxcosx
tanx−cotx
=
sinx
cosx
−
cosx
sinx
=
sin2x
−
cos2x
sinxcosx
=
−cos2x
sinxcosx
を用いると
coshgL
t
=
12
(
e
gL
t
+
e
−
gL
t
)
=
12
(
tan
θ+π
4
+
cot
θ+π
4
)
sinhgL
t
=
12
(
e
gL
t
−
e
−
gL
t
)
=
12
(
tan
θ+π
4
−
cot
θ+π
4
)
より
tanh
gL
t
=
sinh
gL
t
cosh
gL
t
=
−cos
θ+π2
=
sinθ2
--- (21)
が得られる.したがって,時刻
t
における角度は
θ(t)
=
2
sin
−1
(
tanh
gL
t
)
--- (22)
で与えられる.また,その逆関数を考えると,式 (20) は
t(θ)
=
Lg
tanh
−1
(
sinθ2
)
--- (23)
と表すこともできる.
ホーム>>カテゴリー分類>>力学>>質点の力学>>単振り子>>周期の厳密解の導出