等速円運動 (uniform circular motion)

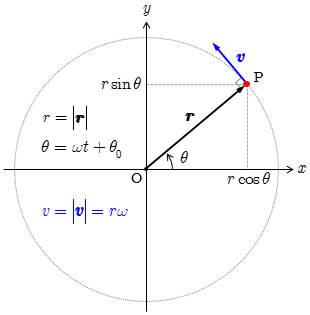
物体が円周上を一定の速さで運動しているとき，その運動を 等速円運動 (uniform circular motion) という．

図のように，点 O を中心とする半径 ${\displaystyle r}$ の円周上を一定の速さ ${\displaystyle v}$ で運動する質点の位置を点 P とする．円運動の回転面を ${\displaystyle xy}$ 平面にとり，平面の極座標（円座標） ${\displaystyle r}$ ，${\displaystyle \theta }$ を用いると点 P の位置ベクトルは

${\displaystyle \mathit{r}=(x,y)=(r\cos \theta ,r\sin \theta )}$     - - - (1)

と表せる． ${\displaystyle \theta }$ は ${\displaystyle +x}$ 軸を基準の方向として測ったベクトル ${\displaystyle \mathit{r}}$ の角度であり，点 P が円周上を回転しているので時間とともに変化する回転角を表す．

質点は一定の速さで回転していることから，回転角 ${\displaystyle \theta (t)}$ の時間変化率（単位時間当たりの回転角）を表す角速度 (angular velocity) ${\displaystyle \omega }$  は

${\displaystyle \omega =\frac{d\theta }{dt}}$ ${\displaystyle =const.}$ （一定）     - - - (2)

であり，時刻 ${\displaystyle t=0}$ で回転角 ${\displaystyle \theta (0)={\theta }_0}$  とすると，式(2)を時間で積分することにより

${\displaystyle \theta (t)=\omega t+{\theta }_0}$     - - - (3)

を得る．したがって，式(1)の各成分は

${\displaystyle x(t)=r\cos (\omega t+{\theta }_0)}$   ，   ${\displaystyle y(t)=r\sin (\omega t+{\theta }_0)}$     - - - (4)

と表される．三角関数の角度部分 ${\displaystyle \omega t+{\theta }_0}$  を 位相 (phase) といい，時刻 ${\displaystyle t=0}$  での位相 ${\displaystyle {\theta }_0}$  を 初期位相 (initial phase) という．

（注1）  通常，回転方向は反時計回りのみを考えて ${\displaystyle \omega >0}$  であるが，時計回りの回転も考慮すると ${\displaystyle \omega <0}$ の場合もありえる．

（注2）  角速度を回転軸方向を向いたベクトル ${\displaystyle \mathit{\omega }}$  とする考え方もある（角速度ベクトル）．この場合，ベクトル ${\displaystyle \mathit{\omega }}$  の向きを進行方向とする右ネジの回る向きが，回転の向きに一致する．つまり，ベクトル ${\displaystyle \mathit{\omega }}$  の先から回転面を見ると，必ず反時計回りの回転運動となる． ${\displaystyle \mathit{\omega }}$  の向きを ${\displaystyle z}$ 軸の正の向きとして， ${\displaystyle xy}$ 平面を等速円運動する点の位置を表すと， ${\displaystyle x(t)=r\cos (\left|\mathit{\omega }\right|t+{\theta }_0)}$  ，  ${\displaystyle y(t)=r\sin (\left|\mathit{\omega }\right|t+{\theta }_0)}$  となる．

• 周期，回転数
• 位置，速度，加速度
• 運動方程式
• シミュレーション

ホーム>>カテゴリー分類>>力学>>質点の力学>>等速円運動

[ページトップ]

利用規約

google translate (English version)