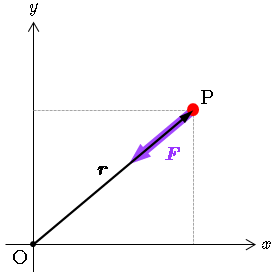
等速円運動 : 運動方程式 (equation of motion)
原点 O を中心として,半径
r
の円周上を角速度
ω>0
(速さ
v=rω
)で等速円運動する質量
m
の質点の位置
r
と加速度
a
の関係は
a=−
ω2r
である (*) ので,この質点の運動方程式は
ma
=
−mω2r
=
−cr
,
c=mω2
- - - (1)
である.よって,
等速円運動する質点には,比例定数
c
(>0)
で位置
r
に比例した,
r
とは逆向きの外力
F=−cr
が作用している.この力は,一定の大きさ
F=|F|
=
|
−m
ω2
r
|
=mr
ω2
=
mv2
r
をもち,常に円の中心を向いているので 向心力である(参照:中心力).
ベクトル
r
,
a
は一般に3次元空間のベクトルである.しかしながら,質点の原点 O のまわりの力のモーメントが
N=
r×F
=r×
(
−cr
)
=−c
(
r×
r
)
=0
であるため,回転運動の法則は
dL
dt
=N=0
を満たし,原点 O のまわりの角運動量
L
が保存する.よって,回転軸の方向(角運動量
L
の方向)は時間に依らず常に一定の方向を向いており,円運動の回転面は固定されている.この回転面を
xy
平面にとれば,ベクトル
r
,
a
の
z
成分は常にゼロなので,2次元の平面ベクトルと考えることができる.
加速度
a=
d2
r/
d
t2
の表記を用いると,等速円運動の運動方程式は
m
d2r
dt2
=−cr
- - - (2)
と表される.成分ごとに書くと
m
d2x
dt2
=−cx
,
m
d2y
dt2
=−cy
- - - (3)
であり,各々独立した定数係数の2階同次線形微分方程式である.
x
成分について,両辺を
m
で割り,
ω2
=
c/m
を用いて整理すると,
d2x
dt2
+
ω2
x
=0
- - - (4)
が得られる.この微分方程式を解くと,その一般解が
x=
Axcos
(
ωt+αx
)
(
Ax
,
αx
: 任意定数)
- - - (5)
のように求まる.同様に,
成分について一般解が
y=
Aycos
(
ωt+αy
)
(
Ay
,
αy
: 任意定数)
- - - (6)
のように求まる.これらの任意定数は,半径
r
の等速円運動であることを考えると,初期位相を
θ0
として,
Ax
=
Ay
=r
,
αx
=
θ0
,
αy
=
θ0
−π2
- - - (7)
となり,
x(t)
=
rcos(
ωt+
θ0
)
,
y(t)
=
rsin(
ωt+
θ0
)
- - - (8)
が得られる.このことから,運動方程式(2)には等速円運動ではない解も存在することがわかる(等速円運動は式(2)を満たす解の特別な場合である).
ホーム>>カテゴリー分類>>力学>>質点の力学>>等速円運動>>運動方程式