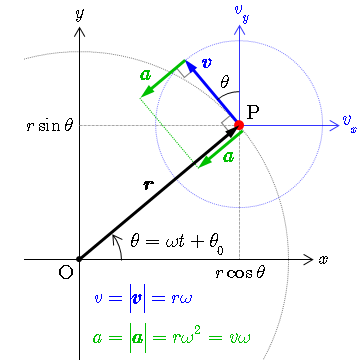
等速円運動 ： 位置 (pisition)，速度 (velocity)，加速度 (acceleration)

原点 O を中心とした半径 r の円周上を角速度 ω で等速円運動する質点の位置 r = ( x  ,  y ) の各成分は

x(t) = rcos( ωt+ θ0 )     - - - (1)
y(t) = rsin( ωt+ θ0 )     - - - (2)

と表される（ θ0 ：初期位相）．質点の速度 v= dr/dt = ( vx  ,  vy ) の各成分は

vx (t) = dx dt = −ωrsin ( ωt+ θ0 )     - - - (3)
vy (t) = dy dt = ωrcos( ωt+ θ0 )     - - - (4)

となる．位置ベクトル r と速度ベクトル v の内積

r⋅v = rcos (ωt+ θ0) { −rωsin (ωt+ θ0) }
             + rsin (ωt+ θ0)  rωcos (ωt+ θ0)
        = −r2ω sin (ωt+ θ0) cos (ωt+ θ0)
             + r2ω sin (ωt+ θ0) cos (ωt+ θ0) =0

より，速度 v は位置 r （動径方向）と直交し，接線方向を向いており，その大きさは

v= vx2 + vy2 = ω2 r2 sin2 ( ωt+ θ0 ) + ω2 r2 cos2 ( ωt+ θ0 ) = r2 ω2 =rω     - - - (5)

である．質点の加速度 a= dv/dt = ( ax  ,  ay ) の各成分は

ax (t) = dvx dt = −ω2rcos ( ωt+ θ0 ) =− ω2 x     - - - (6)
ay (t) = dvy dt = −ω2rsin ( ωt+ θ0 ) =− ω2 y     - - - (7)

となる．上の2式より

a=− ω2r     - - - (8)

であり，この加速度 a は位置 r と逆向きで，常に円の中心 O を向いていることから 向心加速度 (centripetal acceleration) とよばれる．また，加速度の大きさは

a= |a| = | −ω2 r | =rω2 =vω = v2 r     - - - (9)

である．図から分かるように，質点の位置を原点とした速度空間（ vx vy 平面）で考えると， v は，半径 v の円周上を速さ vω で等速円運動していると考えることができる．

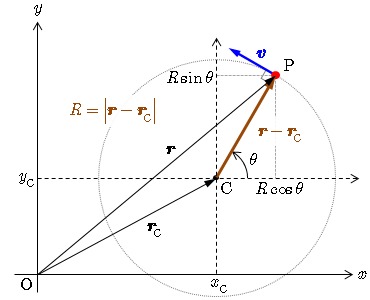
等速円運動の中心を原点 O ではなく任意の点 C ( xC  ,  yC ) とすると，位置ベクトル r の各成分を表す式(1)，式(2)は

x(t) = Rcos( ωt+ θ0 ) +xC     - - - (10)
y(t) = Rsin( ωt+ θ0 ) +yC     - - - (11)

で置き換えられる（ここで，円周の半径を R とした）． xC と yC は定数であるので，速度 v と加速度 a の式は変わらない．この場合，点 C の位置ベクトルを rC = ( xC  ,  yC ) とすると，式(8)は

a=− ω2 ( r− rC )     - - - (12)

と書き換えられる．この場合も加速度は常に中心 C を向いていることになるので，向心加速度には変わりない．

（注）通常，回転方向は反時計回りのみを考えて ω>0  であるが，時計回りの回転も考慮すると ω<0 の場合もありえるので，その場合，式(5)で現れる rω と式(9)で現れる vω については，絶対値 | ω | で置き換える必要がある．

ホーム>>カテゴリー分類>>力学>>質点の力学>>等速円運動>>位置，速度，加速度