基数の定義

■基数と重み

基数とは，数値表現において，各桁の重み付けの基本の数である．

${\displaystyle n}$ 進数の基数は ${\displaystyle n}$ であり，各桁 ${\displaystyle k}$ の重みは ${\displaystyle n^{k-1}}$ となる.

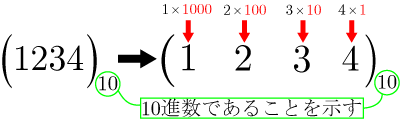
たとえば10進数の234は

${\displaystyle 234=2\times {10}^2+3\times {10}^1+1\times {10}^0}$

${\displaystyle =2\times 100+3\times 10+1\times 1}$

となり，3桁目では重み ${\displaystyle {10}^{3-1}=100}$ が2つあることが分かる．

後述するが，2進数などの ${\displaystyle n}$ 進数についても同じことがいえる．

${\displaystyle {\left(1101\right)}_2=1\times 2^3+1\times 2^2+0\times 2^1+1\times 2^0}$

${\displaystyle =1\times {\left(1000\right)}_2+1\times {\left(100\right)}_2+0\times {\left(10\right)}_2+1\times {\left(1\right)}_2}$

2進数の4桁目の重み ${\displaystyle 2^3={\left(1000\right)}_2}$ が1つあることになる．

■10進数について 

10進数とは0〜9の10個の数字で表現される数字であり，我々が普段の生活で使用している数字である．

1つ上がるごとに重みが，下位の桁の10倍になる．

■2進数について 

コンピュータには人間が使用する10進数が理解できない．そのためコンピュータは電流が流れている状態を1，

電流が流れていない状態を0とした，2個の数字の組み合わせを用いる．これを2進数という．

10進数との対応を下の表に示す．桁が1つ上がるごとに重みが，下位の桁の2倍になる．

■16進数 

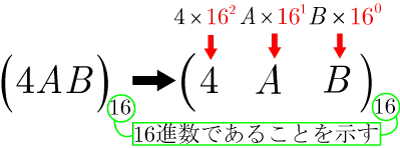
コンピュータが扱う2進数は人間には理解しにくい，そのため人間に理解しやすいように直した表現が16進数である．

16進数は0〜9の10個の数字とA〜Fの6個のアルファベットで表わしたものである．2進数との対応を下の表に示す．

桁が1つ上がるごとに重みが，下位の桁の16倍になる．

 

ホーム>>カテゴリー別分類>>その他>>基数の定義

最終更新日： 2023年10月5日