正弦定理
 三角形の各辺
,
,
と各角
,
,
の間に以下に示す関係がある.
三角形の各辺
,
,
と各角
,
,
の間に以下に示す関係がある.
この関係を,正弦定理という.
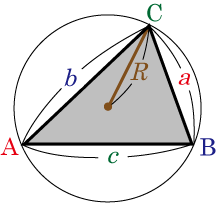
三角形の外接円の半径をとすると,正弦定理は
となる.
■証明
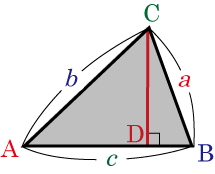 三角形の頂点
から辺
に垂線
を引く.
三角形の頂点
から辺
に垂線
を引く.
直角三角形 と直角三角形 ができる.
直角三角形の辺と三角比より
△ より:
△ より:
式を変形して
よって
・・・・・・(1)
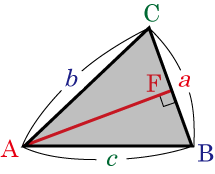
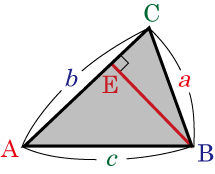 同様にして
同様にして
・・・・・・(2)
・・・・・・(3)
(1),(2),(3)より
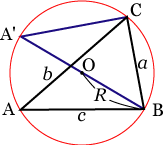 次に,△
の外接円を描き,その円の中心を
,半径を とする.
を延長して外接円と交わる点を
とする. (∵円周角の定理)で,あることより
次に,△
の外接円を描き,その円の中心を
,半径を とする.
を延長して外接円と交わる点を
とする. (∵円周角の定理)で,あることより
→ ,すなわち,
となる.よって,正弦定理は
となる.
最終更新日: 2023年3月10日