概念問題 解答

微積分学　微分

問題4の解答

図1でグラフでは

・$x<0$では，接線の傾きが正になっている．よって，微分したグラフでは，$x<0$ のとき $y>0$ になる．

・$x=0$では，接線の傾きが0になっている．よって，微分したグラフでは，$x=0$ のとき $y=0$ となる．

・$x>0$では，接線の傾きが負になっている．よって，微分したグラフでは，$x>0$ のとき $y<0$ になる．

以上より，微分したグラフは原点を通る右肩下がりのグラフになる．

したがって，答えは2となる．

■参考になるページ

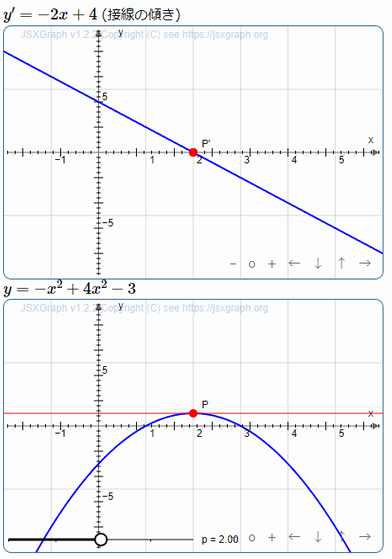
画像をクリックすると，ウェブページにジャンプする．スライダーの○印をドラッグして動かすと点$\text{P}$の位置が移動する．下の図の赤い線が接線である．下の図の2次関数のグラフの頂点の所で接線の傾きが0になり，上の図のグラフが$x$軸と交わる．