概念問題 解答

微積分学　微分

問題6の解答

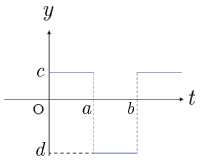
図1のグラフの関数を表すために図に目盛りを入れてみた．この場合，グラフを表す関数は，

${\displaystyle \left\{\begin{array}{ll}{y}^{\prime }=c\hfill & \left(0\leqq t<a\right)\hfill \\ y^{\prime }=d\hfill & \left(a\leqq t<b\right)\hfill \\ y^{\prime }=c\hfill & \left(b\leqq t\right)\hfill \end{array}\right.}$ 　･･････(1)

ただし， ${\displaystyle \left|d\right|>\left|c\right|}$ ， ${\displaystyle d<0}$

となる.(1)を$t$ で積分すると

${\displaystyle \left\{\begin{array}{ll}y=ct+C_1\hfill & \left(0\leqq t<a\right)\hfill \\ y=dt+C_2\hfill & \left(a\leqq t<b\right)\hfill \\ y=ct+C_3\hfill & \left(b\leqq t\right)\hfill \end{array}\right.}$ 　･･････(2)

ただし， ${\displaystyle C_1}$ ， ${\displaystyle C_2}$ ， ${\displaystyle C_3}$ は積分定数

となる．図1の情報だけだと，積分定数の値を定めることはできない．(2)より，各区間の関数は1次関数，すなわち，直線になっている．選択肢はいずれも各区間が直線になっているが，各区間の直線の傾きが異なる．よって，(2)の結果より，各区間の直線の傾きが(2)を満たすものを選べばよい．

• ${\displaystyle 0\leqq t<a}$ のとき：直線の傾きは正
• ${\displaystyle a\leqq t<b}$ のとき：直線の傾きは負
• ${\displaystyle b\leqq t}$ のとき：直線の傾きは正

以上より，答えは1となる．

式を使わずに説明すると

図1より，各区間で微分したものが一定の値になっていることより，各区間の関数は1次関数であることが分かる．そして，その傾きが，正→負→正，に変化しているもとの選ぶとよい．

以上より，答えは1となる．