曲げモーメント（bending moment)

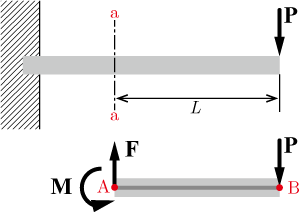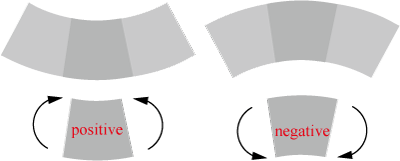
片持ち梁の先端に加重 P を加える．断面 a−a より先端部分を取り出して考えると，剛体のつり合いの考え方より断面には，加重 P とつり合うせん断力 F と加重 P による力のモーメントとつり合う曲げモーメント M が生じている．実際には梁は剛体ではなく弾性体でこの力のモーメントにより梁が曲がるため”曲げ”という言葉が用いられているのだろう．曲げモーメントは力のモーメントと同様にベクトルである．平面図で，曲げモーメントを図示する場合は，図のように円弧に矢印をつけて曲げモーメントによって物体が回転する（曲がる）方向を表す．平面座標で梁の曲げを取り扱う場合は，曲げモーメントはベクトルを使わず曲げモーメントの大きさに正負の符号を付けた値で表す．通常，反時計回りの回転作用を生じさせる曲げモーメントを正の値で表す．

図の場合の曲げモーメント M の値 M を求めてみる（この図では平面内で曲げが生じる場合になるので M は曲げモーメントの大きさに正負の符号を付けた値で表すことにする）．単純化して，梁の重さは考えず，断面 a−a より先端部分を線分ABと見なす．点Aのまわりの力のモーメントのつり合いより

値 M を求めて

M − L P = 0 　　　ただし， | P |=P

よって

M=LP

となる．

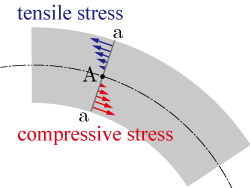断面 a−a の右側の梁に生じる応力に着目すると，曲げモーメントは，梁が荷重等により曲がったときに断面に生じる圧縮応力（compressive stress）と引張応力（tensile stress）による点Aのまわりの力のモーメントの総和になる．

曲げモーメントの正負を梁の曲がり具合で定義することもある．右側断面に生じる曲げモーメントの符号と一致させ，下に凸になる場合を正の曲げモーメント，上に凸の場合を負の曲げモーメントとする．

　

　

　

　

ホーム>>機械工学>>材料力学>>曲げモーメント

最終更新日2018年2月19日