関連するページを見るにはこのグラフ図を利用してください．

梁の曲率半径

梁がたわみ梁の中心線が${\displaystyle Y=Y\left(x\right)}$ という関数で表されるとき${\displaystyle Y\left(x\right)}$ と曲率半径${\displaystyle R}$ との間には

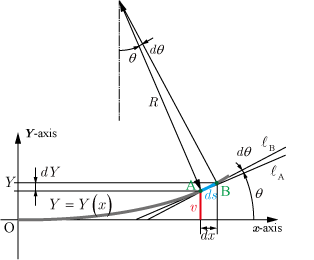
梁が下に凸に変形した場合

${\displaystyle \frac{1}{R}=\frac{d^{2}Y}{d{x}^2}}$

上に凸に変形した場合

${\displaystyle \frac{1}{R}=-\frac{d^{2}Y}{d{x}^2}}$

で表される．

■導出

水平であった梁が上の図のように下に凸に変形した場合について説明する．梁上の点Aでの接線${\displaystyle {\ell }_{\text{A}}}$ と${\displaystyle x}$ 軸とのなす角を${\displaystyle \theta }$ とし，点Aから梁に沿って ${\displaystyle ds}$ だけ離れた点Bでの接線${\displaystyle {\ell }_{\text{B}}}$ と${\displaystyle x}$ 軸とのなす角を${\displaystyle \theta +d\theta }$ とすると

${\displaystyle ds=Rd\theta }$

${\displaystyle \frac{1}{R}=\frac{d\theta }{ds}}$　･･････(1)

となる．ただし，${\displaystyle \theta }$ は${\displaystyle x}$ 軸を基準とし反時計回りを正方向とする.

一方，

${\displaystyle \frac{dY}{dx}=\tan \theta }$　･･････(2)

である．実際の梁では変形量が小さく，${\displaystyle \theta }$ の値も非常に小さな状態で

${\displaystyle \tan \theta \approx \theta }$，${\displaystyle ds\approx dx}$

とみなせる．(1)，(2)は

${\displaystyle \frac{1}{R}=\frac{d\theta }{dx}}$　･･････(3)

${\displaystyle \frac{dY}{dx}=\theta }$　･･････(4)

と書き換えることができる．(4)を(3)に代入すると

${\displaystyle \frac{1}{R}=\frac{d^{2}Y}{d{x}^2}}$　･･････(5)　

が得られる．　

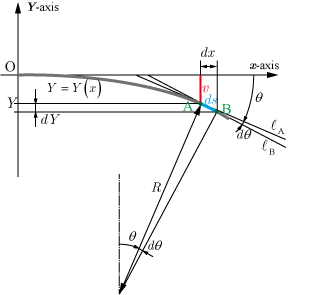次に，2つ目の図のように梁が上に凸にたわむ場合について説明する．下に凸にたわむ場合とことなるのは，${\displaystyle \theta <0}$ で，${\displaystyle dx>0}$のとき，${\displaystyle dY<0}$，${\displaystyle d\theta <0}$ となるので，(1)が

${\displaystyle ds=-Rd\theta }$ ，${\displaystyle \frac{1}{R}=-\frac{d\theta }{ds}}$ 　･･････(6)

となり，(3)が

${\displaystyle \frac{1}{R}=-\frac{d\theta }{dx}}$ 　･･････(7)

となる．よって，(5)が

${\displaystyle \frac{1}{R}=-\frac{d^{2}Y}{d{x}^2}}$　･･････(8)

となる．

${\displaystyle \frac{d^{2}Y}{d{x}^2}}$ は梁の曲率になる.

曲率半径の一般的解説はこのページを参照

　

ホーム>>機械工学>>材料力学>>梁の曲率半径

最終更新日2022年6月9日

[ページトップ]

利用規約

google translate (English version)