微分に関する基本式
| 平均変化率
: |
f(
a+h
)−f(
a
)
h
|
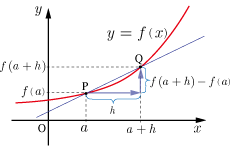
関数
f(
x
)
の
x
の値が,
aから
a+h
に変化したとき,
f(
x
)
の変化量を
x
の増加量
h
で割ったもので,
上図の
直線PQの傾きになる。
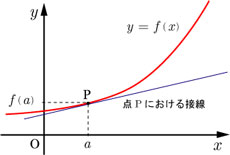
微分係数
:
f
′
(
a
)=
lim
h→0
f(
a+h
)−f(
a
)
h
平均変化率の式で
h
を限りなく0に近づけた時の値で,関数
f(
x
)
の
x=a
における
接線の傾きになる。(点Pにおける接線の傾き)
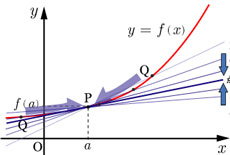
導関数
:
f(
x
)=
lim
h→0
f(
x+h
)−f(
x
)
h
関数
f(
x
)
の導関数とは
f(
x
)
の
x
における微分係数を
x
の関数として表したものである。
戻る
[
ひ]
[
は行]
[
索引トップ]



