増減表
関数
y=f(
x
)
のグラフの概略を描くために,
y=
f
′
(
x
)
の符号を求めて関数
y=f(
x
)
の増加および減少の様子を表にまとめたものが増減表である。
| x
| | a
| | b
| | c
| |
|
f
′
(
x
)
|
+
| 0 |
-
| 0 |
+
| 0 |
-
|
|
f(
x
)
|
↗
|
f(
a
)
極大値 |
↘
|
f(
b
)
極小値 |
↗
|
f(
c
)
極大値 |
↘
|
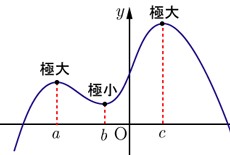
上記の増減表からグラフの概略を描くと,以下のようになる。
 増減表の書き方
増減表の書き方
関数
f(
x
)=
x
3
+3
x
2
−9x+5
を例に増減表の一般的な書き方を説明する。
1.
f
′
(
x
)=0
を満たす x
の値を求める。
※
f
′
(
x
)=0
を満たす xの値で関数
f(
x
)
は極大あるいは極小。
f
′
(
x
)=3
x
2
+6x−9
=3(
x
2
+2x−3
)
=3(
x+3
)(
x−1
)
よって,
f
′
(
x
)=0
を満たすxの値は,
x=−1,3
である。
求めた範囲で増減表を作成すると以下のようになる。
| x
| |
−3
| |
1
| |
|
f
′
(
x
)
| |
0
| |
0
| |
|
f(
x
)
| | | |
| |
2.次に
f
′
(
x
)=0
の符号を書き加え,
f(
x
)
の増減を矢印で示す。
※関数
f(
x
)
は
f(
x
)>0
で増加,関数
f(
x
)
は
f(
x
)<0
で減少。
| x
| |
−3
| |
1
| |
|
f
′
(
x
)
|
+
|
0
|
-
|
0
|
+
|
|
f(
x
)
|
↗
| |
↘
| |
↗
|
3.最後に極値の値を求める。
f(
−3
)=
(
−3
)
3
+3⋅
(
−3
)
2
−9⋅(
−3
)+5
=32
f(
1
)=
(
1
)
3
+3⋅
(
1
)
2
−9⋅(
1
)+5
=0
| x
| |
−3
| |
1
| |
|
f
′
(
x
)
|
+
|
0
|
-
|
0
|
+
|
|
f(
x
)
|
↗
|
32
|
↘
|
0
|
↗
|
f(
x
)=
x
3
+3
x
2
−9x+5
の
グラフはPC版を参照
⇒
戻る
[
そ]
[
さ行]
[
索引トップ]

