|
三角関数の定義 原点を中心として半径 三角関数(正弦,余弦,正接)は,
ただし, ( 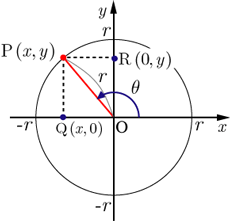 特に,下図の半径が1の場合である円のことを単位円といい,単位円を用いると,
となり, 点
また,
となる。 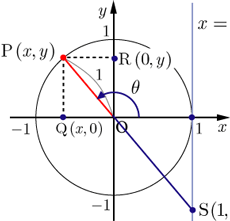 <参照>
戻る [さ] [さ行] [索引トップ] |
|
三角関数の定義 原点を中心として半径 三角関数(正弦,余弦,正接)は,
ただし, (  特に,下図の半径が1の場合である円のことを単位円といい,単位円を用いると,
となり, 点
また,
となる。  <参照>
戻る [さ] [さ行] [索引トップ] |