三角関数の公式(証明)
sin
2
θ+
cos
2
θ=1
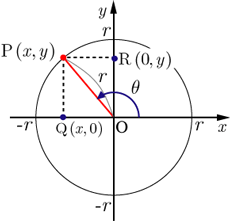
<証明>
三角関数の定義より,
sinθ=
x
r
,cosθ=
y
r
x=rsinθ
・・・(1)
y=rcosθ
・・・(2)
△OQP
において,三平方の定理より,
OQ
2
+
PQ
2
=
OP
2
| x |
2
+
| y |
2
=
r
2
x
2
+
y
2
=
r
2
・・・(3)
(3)に(1)と(2)を代入すると,
sin
2
θ+
cos
2
θ=1
が得られる。
戻る
[さ]
[さ行]
[索引トップ]

|

