余弦定理の証明
三角形の頂点
C
から辺
AB
に垂線
CD
を引く。直角三角形
ACD
と直角三角形
BCD
ができる。(下図)
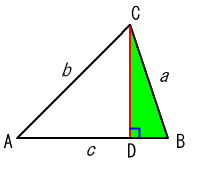直角三角形
BCD
に三平方の定理を用いると，
CB
2
=
CD
2
+
BD
2
･･･(1)
BD=c−bcosA
の関係を，(1)に代入すると
a
2
=
(
bsinA
)
2
+
(
c−bcosA
)
2
=
b
2
sin
2
A+
c
2
−
2cbcosA+
b
2
cos
2
A
=
b
2
(
sin
2
A+
cos
2
A
)+
c
2
−2cbcosA
=
b
2
+
c
2
−2bccosA
∴
a
2
=
b
2
+
c
2
−2bccosA
(
A=90°
，鈍角の場合の証明は省略)
同様にして，
b
2
=
c
2
+
a
2
−2cacosB
(上図)
c
2
=
a
2
+
b
2
−2abcosC
(上図)
も求められる。
戻る
[よ]
[や行]
[索引トップ]
|