■内積の定義

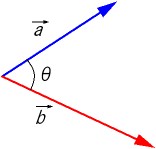
a → ， b → のなす角を θ とするとき，

a → · b → =| a → || b → |cosθ

を a → ， b → の内積という。

a → · b →   代わりに  ( a → , b → )   で表すこともある。

■内積の成分表示

●平面ベクトル（2次元）の場合

内積をベクトルの成分を用いて表す。

a → =( a 1 , a 2 )  ， b → =( b 1 , b 2 )  とすると，

a → · b → = a 1 b 1 + a 2 b 2

となる 。

●空間ベクトル（3次元）の場合

a → =( a 1 , a 2 , a 3 )  ， b → =( b 1 , b 2 , b 3 )  とすると，

a → · b → = a 1 b 1 + a 2 b 2 + a 3 b 3

となる 。

■内積の特徴

特に，a → ， b →  のなす角が90°のとき，

a → · b → =0  （ a 1 b 1 + a 2 b 2 =0 ， a 1 b 1 + a 2 b 2 + a 3 b 3 =0 ）

となる。