ベクトルの大きさと2つのベクトルのなす角
■平面ベクトルの場合(2次元の場合)
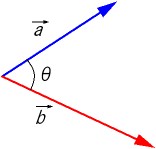
a → =( a 1 , a 2 ) , b → =( b 1 , b 2 ) とすると(ただし,
a
→
≠
0
→
,
b
→
≠
0
→
),
●ベクトルの大きさ
a
→
の大きさを
|
a
→
|
と表す。
| a → | 2 = a → · a → = a 1 2 + a 2 2
●2つのベクトルのなす角
a
→
と
b
→
のなす角を θ
(
0≦θ≦180°
)
とすると,
cos
θ
=
a
→
·
b
→
|
a
→
|
|
b
→
|
=
a
1
b
1
+
a
2
b
2
a
1
2
+
a
2
2
b
1
2
+
b
2
2
■空間ベクトルの場合(3次元の場合)
a
→
=(
a
1
,
a
2
,
a
3
)
, b → =( b 1 , b 2 , b 3 ) とすると(ただし, a → ≠ 0 → , b → ≠ 0 → ),
●ベクトルの大きさ
a → の大きさを | a → | と表す。
| a → | 2 = a → · a → = a 1 2 + a 2 2 + a 3 2
●2つのベクトルのなす角
a → と b → のなす角を θ ( 0≦θ≦180° ) とすると,
cos
θ
=
a
→
·
b
→
|
a
→
|
|
b
→
|
=
a
1
b
1
+
a
2
b
2
+
a
3
b
3
a
1
2
+
a
2
2
+
a
3
2
b
1
2
+
b
2
2
+
b
3
2
[と]
[た行]
[索引トップ]

|