減衰振動 : 散逸関数 (dissipation function)
軸上を減衰振動する質量
の質点には,その位置
に比例した復元力
(
:正定数)が作用する.この力は保存力であり,
を基準点とした位置エネルギー
から
- - - (1)
と求まる.質点の速度
に比例した抵抗力
(
:正定数)についても,ある関数
から
- - - (2)
と求まるように書くことができ,このとき
(
:任意定数)と表される.ここで,
の場合に
としたときの関数
- - - (3)
を 散逸関数 (dissipation function) と呼ぶ.この減衰振動する系の力学的エネルギーは
- - - (4)
であり,力学的エネルギーの時間についての導関数は
- - - (5)
となる.減衰振動する質点の運動方程式は
⇒
- - - (6)
であるので,式(6)を式(5)に代入すると
- - - (7)
が得られる.これは,系の力学的エネルギーが変化する速さが,散逸関数
の−2倍で与えられることを意味する.
なので,時間の経過とともに力学的エネルギーは減少する.すなわち,散逸関数は系のエネルギー散逸の度合いを決める.
と
の関係に応じた3つの場合について散逸関数の式を求める:
(i)
の場合(不足減衰)
位置:
(
,
:定数)
- - - (8)
速度:
- - - (9)
ここで,
は次の2式を満たす角度である.
,
⇒
散逸関数:
- - - (10)
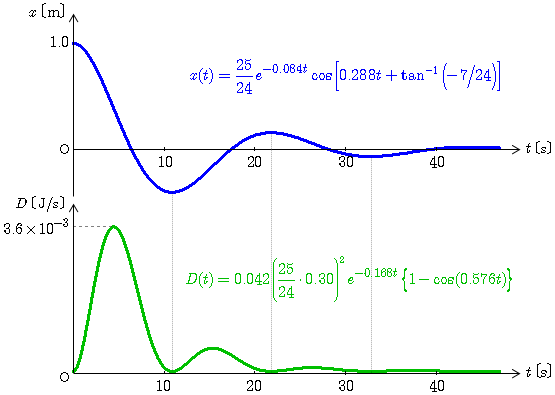
例として,
,
,
,初期条件
,
の場合について,減衰振動する質点の位置
と散逸関数
のグラフを示す.この場合,
,
である.
(ii)
の場合(過減衰)
位置:
(
,
:定数)
- - - (11)
速度:
- - - (12)
⇒
散逸関数:
- - - (13)
(iii)
の場合(臨界減衰)
位置:
(
,
:定数)
- - - (14)
速度:
- - - (15)
⇒
散逸関数:
- - - (16)
ホーム>>カテゴリー分類>>力学>>質点の力学>>減衰振動>>散逸関数
