関連するページを見るにはこのグラフ図を利用してください．

減衰振動 ： 運動方程式 (equation of motion)

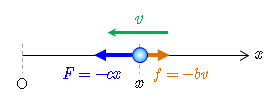
${\displaystyle x}$ 軸上を単振動する質量 ${\displaystyle m}$ の質点には，その位置 ${\displaystyle x}$ に比例した復元力 ${\displaystyle F=-cx}$  （ ${\displaystyle c}$ ：正定数）が作用し，この質点の運動方程式は

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-cx}$     - - - (1)

と表される．この質点に速度 ${\displaystyle v=dx/dt}$ に比例する抵抗力（粘性抵抗）が作用する場合を考える．その比例定数を ${\displaystyle b}$ ${\displaystyle (>0)}$ とすると，この質点の運動方程式は

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-cx-bv}$ ${\displaystyle =-cx-b\frac{dx}{dt}}$     - - - (2)

となる（抵抗力は運動方向（速度方向）とは逆向きであるので，マイナス符号が付いている）．

式(2)において， ${\displaystyle {\omega }_0=\sqrt{c/m}}$ ， ${\displaystyle \gamma =b/2m}$ を導入して整理すると，定数係数の2階同次線形微分方程式

${\displaystyle \frac{d^{2}x}{d{t}^2}+2\gamma \frac{dx}{dt}+{\omega }_0^{2}x=0}$     - - - (3)

が得られる． ${\displaystyle {\omega }_0}$ は抵抗がないときの単振動の角振動数であり， ${\displaystyle \gamma }$ は減衰率という．

この微分方程式を解くと，一般解は ${\displaystyle {\omega }_0}$ と ${\displaystyle \gamma }$ の関係に応じて以下の3つの場合に分けられる：

(i)  抵抗が比較的小さくて ${\displaystyle \gamma <{\omega }_0}$ の場合（不足減衰 : under damping）

${\displaystyle x=A{e}^{-\gamma t}\cos (\omega t+\alpha )}$   ，   ${\displaystyle \omega =\sqrt{{\omega }_0^2-{\gamma }^2}}$     - - - (4)

${\displaystyle A}$ と ${\displaystyle \alpha }$ は任意定数である．

(ii)  抵抗が比較的大きくて ${\displaystyle \gamma >{\omega }_0}$ の場合（過減衰 : over damping）

${\displaystyle x=e^{-\gamma t}\left(c_1{e}^{\eta t}+c_2{e}^{-\eta t}\right)}$   ，   ${\displaystyle \eta =\sqrt{{\gamma }^2-{\omega }_0^2}}$     - - - (5)

${\displaystyle c_1}$ と ${\displaystyle c_2}$ は任意定数である．

(iii)  ${\displaystyle \gamma ={\omega }_0}$ の場合（臨界減衰 : critical damping）

${\displaystyle x=\left(c_1+c_{2}t\right)e^{-\gamma t}}$     - - - (6)

${\displaystyle c_1}$ と ${\displaystyle c_2}$ は任意定数である．

${\displaystyle {\omega }_0=0.30{\text{s}}^{\text{-1}}}$  として，同じ初期条件 ${\displaystyle x_0=1.0\text{m}}$ ，${\displaystyle v_0=0\text{m/s}}$  の下で， ${\displaystyle \gamma }$ を不足減衰（ ${\displaystyle \gamma =0.084,0.18{\text{s}}^{-1}}$ ）の状況から臨界減衰（ ${\displaystyle \gamma =0.30{\text{s}}^{-1}}$ ），過減衰（ ${\displaystyle \gamma =0.50,0.78{\text{s}}^{-1}}$ ）の状況に変えたときのグラフを下図に示す．

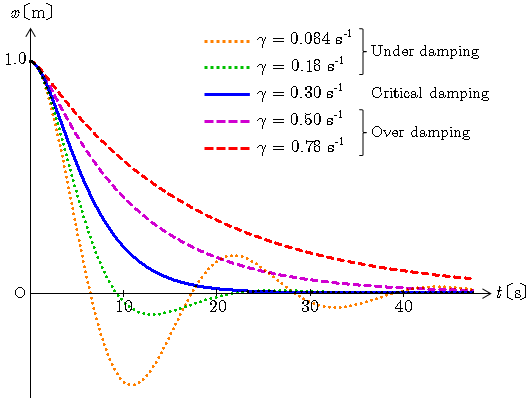
それぞれのグラフの式は以下のとおりである．

${\displaystyle \gamma =0.084{\text{s}}^{-1}}$  （不足減衰）    ⇒     ${\displaystyle x=\frac{25}{24}{e}^{-0.084t}\cos \left(0.288t+{\tan }^{-1}\left(-7/24\right)\right)}$

${\displaystyle \gamma =0.18{\text{s}}^{-1}}$  （不足減衰）    ⇒     ${\displaystyle x=\frac{5}{4}{e}^{-0.18t}\cos \left(0.24t+{\tan }^{-1}\left(-3/4\right)\right)}$

${\displaystyle \gamma =0.30{\text{s}}^{-1}}$  （臨界減衰）    ⇒     ${\displaystyle x=(1.0+0.3t)e^{-0.30t}}$

${\displaystyle \gamma =0.50{\text{s}}^{-1}}$  （過減衰）    ⇒     ${\displaystyle x=\frac{9}{8}{e}^{-0.10t}-\frac{1}{8}{e}^{-0.90t}}$

${\displaystyle \gamma =0.78{\text{s}}^{-1}}$  （過減衰）    ⇒     ${\displaystyle x=\frac{25}{24}{e}^{-0.060t}-\frac{1}{24}{e}^{-1.5t}}$

不足減衰の状態（ ${\displaystyle \gamma <{\omega }_0}$ ）から抵抗を強く（ ${\displaystyle \gamma }$ を大きく）していくと， ${\displaystyle e^{-\gamma t}}$  により振動の減衰が大きくなり，ついには振動しない臨界減衰（ ${\displaystyle \gamma ={\omega }_0}$ ）に至る．さらに抵抗を強くしていくと，抵抗が強くなりすぎて動きが鈍くなり， ${\displaystyle e^{-(\gamma -\eta )t}}$  のためになかなか釣り合いの位置（ ${\displaystyle x=0}$ ）に近づかない過減衰（ ${\displaystyle \gamma >{\omega }_0}$ ）に至る．臨界減衰のときが最も減衰が速い．

ホーム>>カテゴリー分類>>力学>>質点の力学>>減衰振動>>運動方程式

[ページトップ]

利用規約

google translate (English version)