|
減衰振動 : 過減衰 (over damping)
軸上を単振動する質量 の質点に速度 に比例する抵抗力が作用するときの運動方程式
( , :正定数) - - - (1)
において,単振動の角振動数 と減衰率 を導入して整理すると,定数係数の2階同次線形微分方程式
- - - (2)
が得られる.この特性方程式 の解 は,抵抗が比較的大きくて ならば2つの異なる実数根となり,この場合を過減衰 (over damping) という. とおくと,式(2)の一般解は
( , :任意定数) - - - (3)
で与えられ, なので が無限に大きくなるとゼロに近づく.この解は振動せずに釣り合いの位置( )に収束する非周期的減衰 (aperiodic damping) を示す.質点の速度は
- - - (4)
であり,初期条件として, , を考えると,任意定数 と は
, - - - (5)
を満たすように決定される.
, として,正の初期位置( )と負の初期位置( )の場合について,各々4通りの初期速度で計算した過減衰のグラフを下図に示す.
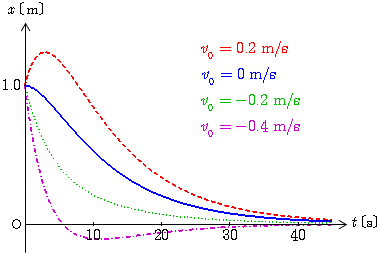
正の初期位置
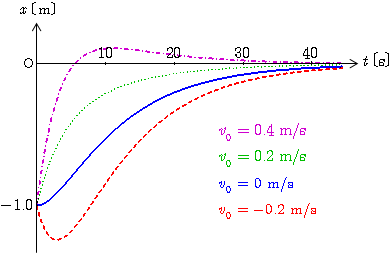
負の初期位置
式(3)において, となる時刻は, ⇒ より
- - - (6)
となる. なので, であれば必ず一度釣り合いの位置( )を通過し, であれば一度も釣り合いの位置を通過しない.
また,式(4)において,速度 とおくと位置 が極大または極小になるときの時刻が得られる.その時刻は, ⇒ より
- - - (7)
となる. なので,
であれば,位置 がどこかの時点で極大または極小となる.