モンキー・ハンティング (monkey hunting)
モンキー・ハンティング (monkey hunting) とは「銃を持ったハンターが木から落ちたサルを狙ったときに,どのように銃を撃てば弾丸がサルにあたるか?」という問題である.
図1のように,水平方向に 軸,鉛直上向きに 軸をとり,原点 にある小球 を 軸とのなす角 の方向に,時刻 において,初速度 で位置 にある小球 を狙って投射した.それと同時に,小球 を初速ゼロで落下させた.重力加速度の大きさを とし,空気抵抗を無視できるものとする.
この状況において,ある時刻で小球 (弾丸)が必ず小球 (サル)と衝突することを以下で見ていく.
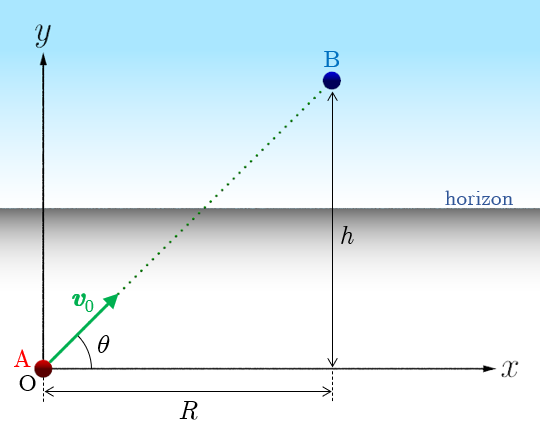
図1
小球 を狙って小球 を投射しているので,角 は
を満たす.小球 の初速度の大きさを とすると,初速度 なので,小球 の 座標が に達するまでの,時刻 における小球 の位置 は
,
と表される(加速度 の等加速度運動).また,小球 の位置 は
,
と表される.このとき,図2に示すように,重力の影響による2つの小球の落下距離は共に である.小球 から小球 へのベクトルは
となるので,小球 と小球 を結ぶ直線はどの時刻においても常に初速度 に平行,つまり,水平面に対して を満たす方向となっている.
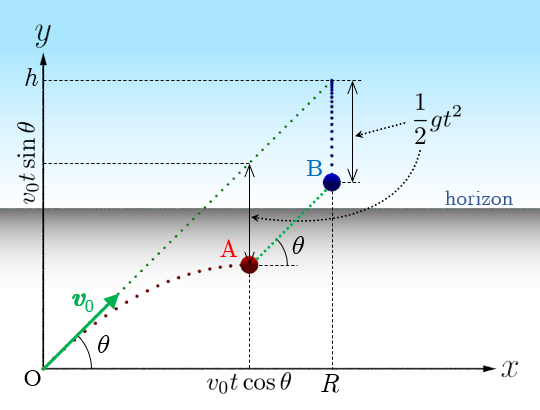
図2
上式において のとき,つまり,時刻 において,2つの小球の位置は一致し,衝突する(図3).このとき,小球 が落下した距離は
となる.したがって,小球 が地面に到達する前に衝突が起こるための,初速 の満たす条件は
より
である.
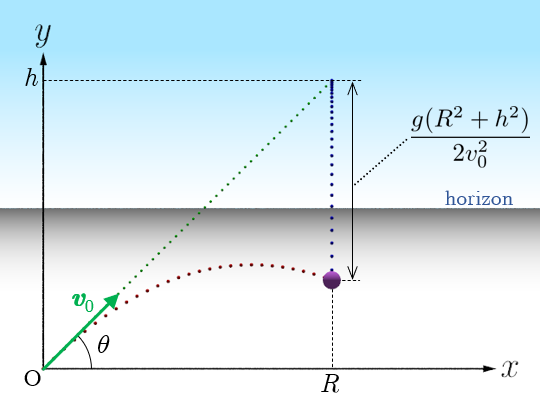
図3
下にモンキー・ハンティングのアニメーションを示す.右側は小球 (青球)から小球 (赤球)を見たときの視点でのアニメーションを示している.2つの小球が衝突するまで,小球 から見た小球 の相対速度は常に であるので,小球 が直線的に速さ で接近してくるように見える.(※ アニメーションでは,赤球と青球の位置が一致しても,衝突させずにすり抜けさせている.)
小球 を狙って小球 を投射したときに,2つの小球が衝突する様子をモンキー・ハンティングのシミュレーションで確認してみよう.