関連するページを見るにはこのグラフ図を利用してください．

単振動 ： 力学的エネルギー (mechanical energy)

角振動数 ${\displaystyle \omega }$ で単振動する質量 ${\displaystyle m}$ の質点の位置 ${\displaystyle x}$ を

${\displaystyle x(t)=A\cos (\omega t+\alpha )}$     - - - (1)

と表すと，質点の速度 ${\displaystyle v}$ は

${\displaystyle v(t)=\frac{dx}{dt}=-\omega A\sin (\omega t+\alpha )}$     - - - (2)

であるので，質点の運動エネルギーは

${\displaystyle K=\frac{1}{2}m{v}^2}$ ${\displaystyle =\frac{1}{2}m{\left\{-A\omega \sin (\omega t+\alpha )\right\}}^2}$ ${\displaystyle =\frac{1}{2}m{\omega }^2{A}^2{\sin }^2(\omega t+\alpha )}$     - - - (3)

となり，基準点を ${\displaystyle x=0}$ としたときの位置エネルギーは

${\displaystyle U=\frac{1}{2}c{x}^2}$ ${\displaystyle =\frac{1}{2}m{\omega }^2{\left\{A\cos (\omega t+\alpha )\right\}}^2}$ ${\displaystyle =\frac{1}{2}m{\omega }^2{A}^2{\cos }^2(\omega t+\alpha )}$     - - - (4)

となる．ここで， ${\displaystyle c=m{\omega }^2}$  を用いた．したがって，単振動する質点の力学的エネルギーは

${\displaystyle E=K+U}$ ${\displaystyle =\frac{1}{2}m{\omega }^2{A}^2\left\{{\sin }^2(\omega t+\alpha )+{\cos }^2(\omega t+\alpha )\right\}}$ ${\displaystyle =\frac{1}{2}m{\omega }^2{A}^2}$     - - - (5)

となり，角振動数 ${\displaystyle \omega }$ の2乗と振幅 ${\displaystyle A}$ の2乗に比例する．また，力学的エネルギーは定数で表され，常に一定であるので保存することが分かる．

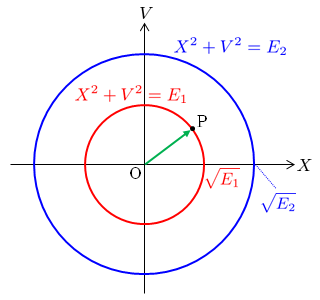
2つの新たな変数 ${\displaystyle X}$ ， ${\displaystyle V}$ を次のように定義する．

${\displaystyle X\equiv \sqrt{\frac{c}{2}}x}$ ${\displaystyle =\sqrt{E}\cos (\omega t+\alpha )}$     - - - (6)
${\displaystyle V\equiv -\sqrt{\frac{m}{2}}v}$ ${\displaystyle =\sqrt{E}\sin (\omega t+\alpha )}$     - - - (7)

ここで，式 (5) より ${\displaystyle E=m{\omega }^2{A}^2/2}$ を用いた．また，式 (3)，(4) より  ${\displaystyle V^2=K}$ ， ${\displaystyle X^2=U}$  である．すると，

${\displaystyle X^2+V^2=E}$     - - - (8)

なので，上式は ${\displaystyle XV}$ 平面における半径 ${\displaystyle \sqrt{E}}$ の円を表し，その平面で点 ${\displaystyle P(X,V)}$ は半径 ${\displaystyle \sqrt{E}}$ の円周上を角速度 ${\displaystyle \omega }$ で等速円運動している．

式 (6)，(7) の定義から分かるように， ${\displaystyle X}$ と ${\displaystyle V}$ はそれぞれ単振動の規格化された位置と速度を表す（次元はともにエネルギーの平方根）．力学的エネルギー ${\displaystyle E}$ が保存するような運動では， ${\displaystyle E}$ を一定に保つように位置と速度が変化するのであるが，単振動では式 (6)，(7) で規格化された位置 ${\displaystyle X}$ と速度 ${\displaystyle V}$ が ${\displaystyle XV}$ 平面において半径 ${\displaystyle \sqrt{E}}$ の円周上を等速円運動するように変化することを式 (8) は意味している．単振動の角振動数 ${\displaystyle \omega }$ や振幅 ${\displaystyle A}$ が大きくなって力学的エネルギーが増大すると， ${\displaystyle XV}$ 平面でより大きな半径の円周上を運動することとなる．

位置と速度（もしくは運動量）を座標軸にとった空間を物理学における位相空間という．質点の運動状態を定めるには位置と速度が必要であり，その運動は位相空間において一本の曲線で表現できる．

ホーム>>カテゴリー分類>>力学>>質点の力学>>単振動>>位置エネルギー

[ページトップ]

利用規約

google translate (English version)