関連するページを見るにはこのグラフ図を利用してください．

単振動 ： 位置 (postion)，速度 (velocity)，加速度 (acceleration)

角振動数 ${\displaystyle \omega }$ で単振動する質点の位置 ${\displaystyle x}$ を

${\displaystyle x(t)=A\cos (\omega t+\alpha )}$     - - - (1)

と表すと，質点の速度 ${\displaystyle v}$ は

${\displaystyle v(t)=\frac{dx}{dt}=-\omega A\sin (\omega t+\alpha )}$     - - - (2)

となり，質点の加速度 ${\displaystyle a}$ は

${\displaystyle a(t)=\frac{dv}{dt}=-{\omega }^{2}A\cos (\omega t+\alpha )}$     - - - (3)

となる．このとき，加速度の式には位置 ${\displaystyle x}$ と同じ表式  ${\displaystyle A\cos (\omega t+\alpha )}$  が含まれるので，加速度と位置の関係は

${\displaystyle a(t)=-{\omega }^{2}x(t)}$     - - - (4)

と表せて，加速度は位置 ${\displaystyle x}$ に比例し，逆向きであることがわかる．単振動において，上式は常に成り立つ．

速度の式(2) および加速度の式(3) より，速度の大きさの最大値 ${\displaystyle v_{\max }}$ と加速度の大きさの最大値 ${\displaystyle a_{\max }}$ はそれぞれ，

${\displaystyle v_{\max }=A\omega }$ ， ${\displaystyle a_{\max }=A{\omega }^2}$     - - - (5)

である．

${\displaystyle A=1.0\text{m}}$ ， ${\displaystyle \omega =1.0{\text{s}}^{-1}}$ ， ${\displaystyle \alpha =0}$ の場合について，位置 ${\displaystyle x〔\text{m}〕}$ ，速度 ${\displaystyle v〔\text{m/s}〕}$ ，加速度 ${\displaystyle a〔{\text{m/s}}^2〕}$ のグラフを描くと下図のようになる．

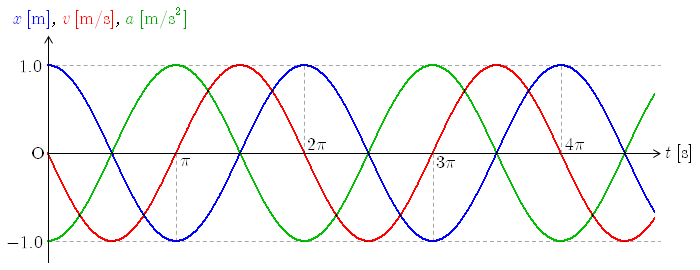
図からも分かるように，位置と速度は位相が ${\displaystyle \pi /2}$ ずれ，位置と加速度は位相が ${\displaystyle \pi }$ ずれている． 横軸に質点の位置 ${\displaystyle x}$ をとり，時刻 ${\displaystyle t=0\text{s}}$ から ${\displaystyle t=\pi 〔\text{s}〕}$ までの単振動のイメージを下図に示す．

水色の球が質点を表し，各位置における速度と加速度をそれぞれ赤矢印と緑矢印，および数値で示している．速度の大きさは原点で最大になり，加速度の大きさは振動の両端で最大となる．

他の表式においても， ${\displaystyle a=-{\omega }^{2}x}$  が成り立つか否かを確かめてみる．位置を

${\displaystyle x(t)=A\sin (\omega t+\beta )}$

とすると，速度と加速度は

${\displaystyle v(t)=\frac{dx}{dt}=\omega A\cos (\omega t+\beta )}$ ， ${\displaystyle a(t)=\frac{dv}{dt}=-{\omega }^{2}A\sin (\omega t+\beta )}$

となり， ${\displaystyle a=-{\omega }^{2}x}$  が成り立つ．また，位置を

${\displaystyle x(t)=A_1\cos \omega t+A_2\sin \omega t}$

とすると，速度と加速度は

${\displaystyle v(t)=\frac{dx}{dt}=-\omega A_1\sin \omega t+\omega A_2\cos \omega t}$ ， ${\displaystyle a(t)=\frac{dv}{dt}=-{\omega }^2{A}_1\cos \omega t-{\omega }^2{A}_2\sin \omega t=-{\omega }^2(A_1\cos \omega t+A_2\sin \omega t)}$

となり，同様に ${\displaystyle a=-{\omega }^{2}x}$  が成り立つ．

式(1)では，振動の中心を原点（ ${\displaystyle x=0}$ ）としているが，振動の中心を任意の点 ${\displaystyle x=x_{\text{C}}}$ とすると，式(1)は

${\displaystyle x(t)=A\cos (\omega t+\alpha )+x_{\text{C}}}$     - - - (6)

で置き換えられる． ${\displaystyle x_{\text{C}}}$ は定数であるので，速度 ${\displaystyle v}$ と加速度 ${\displaystyle a}$ の式は変わらない．この場合，式(4)は

${\displaystyle a(t)=-{\omega }^2(x-x_{\text{C}})}$     - - - (4)

と書き換えられる．よって，加速度は中心位置からの変位 ${\displaystyle x-x_{\text{C}}}$ に比例し，変位と逆向きとなる．

ホーム>>カテゴリー分類>>力学>>質点の力学>>単振動>>位置，速度，加速度

[ページトップ]

利用規約

google translate (English version)