関連するページを見るにはこのグラフ図を利用してください．

ばね‐質量系 ： 鉛直ばね振り子(vertical spring pendulum)

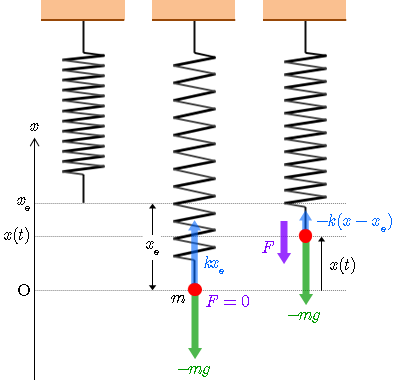
図のように，質量 ${\displaystyle m}$ の質点（赤丸）を先端に付けたばねを鉛直に吊るして静止させたとき，質点に働く重力によりばねは自然長から ${\displaystyle x_{\text{e}}}$ だけ伸びたとすると，鉛直上向きの弾性力 ${\displaystyle k{x}_{\text{e}}}$ と下向きの重力 ${\displaystyle mg}$ が釣り合うため，次式が成り立つ．

${\displaystyle k{x}_{\text{e}}-mg=0}$     - - - (1)

このつり合いの位置を原点 O として鉛直上向きに ${\displaystyle x}$ 軸をとり，時刻 ${\displaystyle t}$ での質点の位置を ${\displaystyle x(t)}$ とする．このとき，ばねの自然長からの変化量は ${\displaystyle x-x_{\text{e}}}$ なので，ばねの弾性力は ${\displaystyle -k(x-x_{\text{e}})}$ となる．質点に作用する力 ${\displaystyle F}$ は，ばねの弾性力と重力との合力なので

${\displaystyle F=-k(x-x_{\text{e}})-mg}$ ${\displaystyle =-kx+k{x}_{\text{e}}-mg}$
   ${\displaystyle =-kx}$     - - - (2)

となる（釣り合いの位置を原点 O にとると，質点に作用する力について重力の影響は考慮しなくてよい）．したがって，力 ${\displaystyle F}$ を受けて ${\displaystyle x}$ 軸上を運動する質量 ${\displaystyle m}$ の質点の運動方程式は次式となる．

${\displaystyle m\frac{d^{2}x}{d{t}^2}=-kx}$     - - - (3)

上式の両辺を ${\displaystyle m}$ で割り，

${\displaystyle \omega =\sqrt{\frac{k}{m}}}$     - - - (4)

とおいて整理すると，運動方程式は

${\displaystyle \frac{d^{2}x}{d{t}^2}+{\omega }^{2}x=0}$     - - - (5)

と表され，単振動の従う微分方程式の標準形が得られる．この微分方程式の一般解は

${\displaystyle x(t)=A\cos (\omega t+\alpha )}$    （ ${\displaystyle A,\alpha }$ ： 任意定数）     - - - (6)

であり， ${\displaystyle \omega =\sqrt{k/m}}$ がこのばね‐質量系の固有角振動数となる．この単振動の周期は次式で表される．

${\displaystyle T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{m}{k}}}$     - - - (7)

したがって，周期 ${\displaystyle T}$ は質量 ${\displaystyle m}$ が大きく（小さく）なると， ${\displaystyle \sqrt{m}}$ で大きく（小さく）なり，ばね定数 ${\displaystyle k}$ が大きく（小さく）なると， ${\displaystyle 1/\sqrt{k}}$ で小さく（大きく）なる．

質点の速度は  ${\displaystyle v(t)=dx/dt=-\omega A\sin (\omega t+\alpha )}$  と表されるので，初期条件として，時刻 ${\displaystyle t=0}$ のときの質点の位置を  ${\displaystyle x(0)=x_0}$  ，質点の速度を  ${\displaystyle v(0)=v_0}$  とすると，

${\displaystyle x(0)=A\cos \alpha =x_0}$     - - - (8)

${\displaystyle v(0)=-\omega A\sin \alpha =v_0}$     - - - (9)

より，任意定数 ${\displaystyle A}$ ， ${\displaystyle \alpha }$ は

${\displaystyle A^2={(A\cos \alpha )}^2+{(A\sin \alpha )}^2}$ ${\displaystyle =x_0^2+{\left(-\frac{v_0}{\omega }\right)}^2=x_0^2+\frac{v_0^2}{{\omega }^2}}$     - - - (10)

${\displaystyle \tan \alpha =\frac{\sin \alpha }{\cos \alpha }=\frac{-\frac{v_0}{\omega }}{x_0}=-\frac{v_0}{x_0\omega }}$      ${\displaystyle (x_0\ne 0)}$     - - - (11)

を満たすように決定する（ ${\displaystyle x_0=0}$ のときは， ${\displaystyle \cos \alpha =0}$ を満たす ${\displaystyle \alpha }$ を考えればよい ）．

基準点を原点 O （ ${\displaystyle x=0}$ ）としたときの，質点に働く合力 ${\displaystyle F=-kx}$ による位置エネルギーは  ${\displaystyle U(x)=\frac{1}{2}k{x}^2}$  である（重力もばねの弾性力も保存力なので，合力 ${\displaystyle F}$ も保存力）．これはばねの弾性力 ${\displaystyle -k(x-x_{\text{e}})}$ による位置エネルギー

$U_e(x)=-{\displaystyle {\int }_0^x\left\{-k(x-x_e)\right\}}dx$ ${\displaystyle =\frac{1}{2}k{\left[{(x-x_e)}^2\right]}_0^x}$ ${\displaystyle =\frac{1}{2}k{x}^2-k{x}_{e}x}$     - - - (12)

と，重力 ${\displaystyle -mg}$ による位置エネルギー

$U_g(x)=-{\displaystyle {\int }_0^x(-mg)}dx$ ${\displaystyle =mgx}$ ${\displaystyle =k{x}_{e}x}$     - - - (13)

の和 ${\displaystyle U(x)=U_e(x)+U_g(x)}$ である．ここで，釣り合いの式 ${\displaystyle mg=k{x}_{\text{e}}}$ を用いた．

例として，質点の質量 ${\displaystyle m=2.0\text{kg}}$ ，ばね定数 ${\displaystyle k=8.0\text{N/m}}$ の場合， ${\displaystyle \omega =\sqrt{k/m}}$ ${\displaystyle =\sqrt{8.0/2.0}=2.0{\text{s}}^{\text{-1}}}$  より，単振動の一般解は

${\displaystyle x(t)=A\cos (2.0t+\alpha )}$    （ ${\displaystyle A,\alpha }$ ： 任意定数）     - - - (14)

となる．初期条件として，時刻 ${\displaystyle t=0\text{s}}$ で位置 ${\displaystyle x(0)=5.0\text{m}}$ ，速度 ${\displaystyle v(0)=0.0\text{m/s}}$  とすると，

${\displaystyle A^2={5.0}^2}$  ，  ${\displaystyle \tan \alpha =0}$   ⇒   ${\displaystyle A=5.0\text{m}}$  ，  ${\displaystyle \alpha =0}$     - - - (15)

となり，初期条件を満たす解が

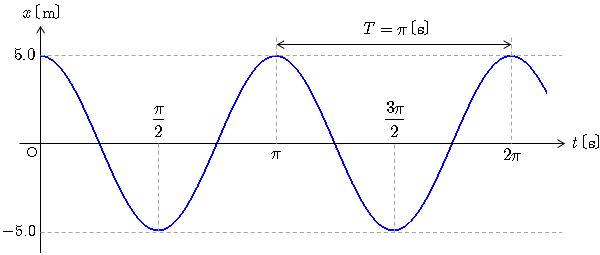
${\displaystyle x(t)=5.0\cos 2.0t〔\text{m}〕}$     - - - (16)

と求まる．周期は  ${\displaystyle T=2\pi /\omega }$ ${\displaystyle =2\pi /2.0=\pi 〔\text{s}〕}$s である．

ホーム>>カテゴリー分類>>力学>>質点の力学>>単振動>>ばね‐質量系>>鉛直ばね振り子

最終更新日：2022年12月20日

[ページトップ]

利用規約

google translate (English version)