�V�����f�B���K�[������
�V�����f�B���K�[�������̒����F�X�e�b�v�|�e���V����
�|�e���V���������^������d�q�ɑ����V�����f�B���K�[�������́C
�V�����f�B���K�[�������� ��������ƁC
�萔���� �Ƃ��āC�ϐ������Ƃ���ƁC
�ϐ� �C �̎��ɕ��������̂ŁC�Δ���������ŕ\���C �Ɋւ��Ĉȉ��̎���D
���}�̂悤�ȃX�e�b�v�|�e���V����
�ɂ����āC(A)�̉𥥥(B)�����߂�D
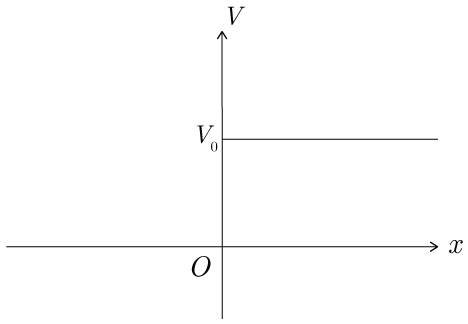
[�T]
�̂Ƃ�
���C
�d�ˍ��킹�̌������C
[�U]
�̂Ƃ�
���C
�d�ˍ��킹�̌������C
����( )����d�q����˂����Ƃ��C �̗̈�ł́C���ˊp�Ɣ��ˊp�C �̗̈�ł́C���ߔg�݂̂̉��ɂȂ�D
���_ �̋��E�������������߂�D
�g���� �͌��_ �œ������Ȃ邽��
�܂��C����
�͌��_ �œ������Ȃ邽��
����āC�W����
�C
������
�C
[1]
�̏ꍇ
���ˊp�̃G�l���M�[���|�e���V�����̃G�l���M�[���傫���Ƃ��C
�͎����ɂȂ�D���������āC���˔g �̈ꕔ�͔��˂�(���˔g )�C�ꕔ�͓��ߔg �Ƃ��āC �̗̈�ɓ`������(���})�D
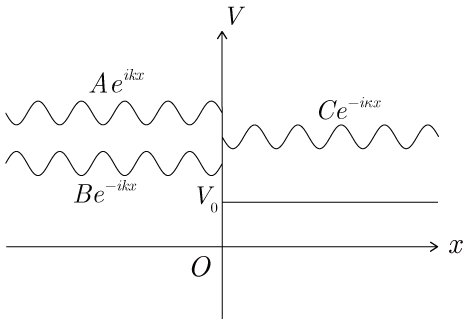
[2]
�̏ꍇ
���˔g�̃G�l���M�[���|�e���V�����̃G�l���M�[��菬�����Ƃ��C
�͋����ɂȂ�D���ߔg��
�Ƃ��āC �̗̈�Ŏw�����I�Ɍ�������D���������āC���˔g �́C �̗̈�Ɏw�����I�Ɍ������Ȃ���N��������C���˂���D(���˔g )(���})�D
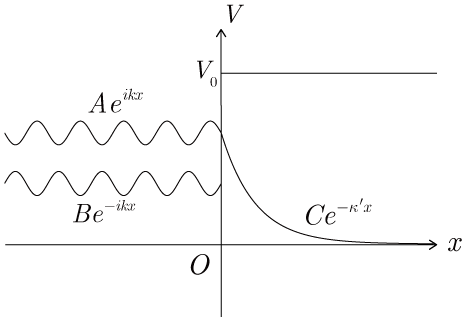
�V�����f�B���K�[�������̒����F�X�e�b�v�|�e���V�����̏ꍇ�i�C������j
�ꎟ������^�����鎩�R���q���V�����f�B���K�[�������́C
�V�����f�B���K�[�������� ���������
�ȉ��̊W����������D
�A�C���V���^�C���E�h���u���C�̊W�� �C ���
����́C�Θ_�I�ȃG�l���M�[��\���D
�A�C���V���^�C���E�h���u���C�̊W��
�C
��p���āC���R���q���V�����f�B���K�[�������̉��́C�ȉ��ŕ\�����D
�z�[��>>�ʎq�͊w>>�ꎟ���V�����[�f�B���K�[�������̃X�e�b�v�|�e���V�����̒���
�w���X�^�b�t�쐬
2024�N12��23��