質量
m [
kg ]
の質点が
z
軸の周りを半径
r
[ m ]
の円軌道を描いて回転するとき,
z
軸のまわりの慣性モーメント
I
は次式となる.
I=m
r2
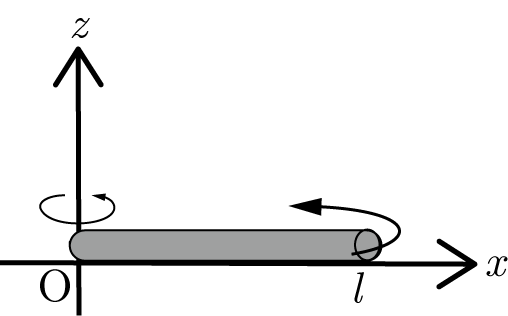
今回の問題のように連続体の慣性モーメントを求める場合,図のように棒を細分化し,微小部分(微小質量
dm
)の集合体として考える.それぞれの微小部分の
z
軸からの距離を
x
(
0≤x≤l
)
としたとき,距離
x
の位置にある微小部分の,
z
軸のまわりの微小慣性モーメント
dI
は,
dI=
x
2
dm
となる.この一様な棒の線密度(単位長さ当たりの質量)を
λ
とすると
dm
は微小長さ
dx×
線密度
λ
で表せる.棒の
質量は
M
,長さは
l
なので,この棒の線密度は,
λ=
M
l
[
kg/m ]
となるので,微小質量は
dm=λdx
=
M
l
dx
となる.棒の慣性モーメントは,この微小慣性モーメント
dI
を
x
が0から
l
まで足し合わせる(積分する)ことで求められる.したがって
I=∫dI=∫
x
2
dm=
∫
0
l
x
2
M
l
dx
=
M
l
[
x
3
3
]
0
l
=
M
l
(
l
3
3
−
0
3
)=
M
l
2
3
を得る.
閉じる