斜面を速く転がり落ちる順番

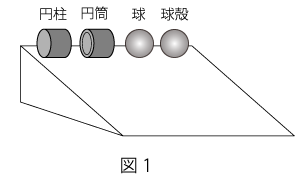
剛体の回転軸のまわりの慣性モーメントが大きいほど，その剛体は回転しにくい．したがって，斜面を滑らずに転がる場合，重心を通る回転軸のまわりの慣性モーメントが大きい剛体ほど遅く転がり落ちる．これらの剛体の，重心を通る回転軸のまわりの慣性モーメントを小さい順に並べると，

2 5 M R 2 (球) < 1 2 M R 2 (円柱) < 2 3 M R 2 (球殻) <M R 2 (円筒)

となる．したがって，球，円柱，球殻，円筒の順に速く転がり落ちる．

より詳細に考えてみよう．
重心を通る回転軸のまわりの剛体の慣性モーメントを IG とすると，水平面とのなす角 β の斜面を転がり落ちる剛体の重心の加速度 A [ m/s2] は

A= gsinβ 1+ IG MR2

と表される．ここで， g [ m/s2] は重力加速度の大きさである．したがって，これらの剛体についての慣性モーメント IG を代入して，重心の加速度の大きい順に並べると

57 gsinβ (球) > 23 gsinβ (円柱) > 35 gsinβ (球殻) > 12 gsinβ (円筒)

となる．つまり，重心の進む速さの順番は，半径 R [ m] ，質量 M [ kg] に関係なく，剛体の形状で決まる．

閉じる