| ||
|
気体分子の運動と圧力
気体分子は熱運動によって空間中を不規則に飛び回りながら,壁にぶつかっては跳ね返る動きを繰り返している.気体分子は壁にぶつかって跳ね返るとき,その壁に力を及ぼす.単位面積当たりに気体全体が壁べに及ぼす力を気体の圧力という.ここでは,気体分子に着目して気体の運動について考える.
単純化のため気体については以下の条件を満たしているものとする.- 気体は理想気体とする.
- 分子同士の衝突は考えず,壁と分子の衝突のみ考える.
- 分子と壁の衝突は弾性衝突とする.つまり,衝突後の速さは変化しない.
- 空間中には膨大な数の分子が飛び回っており,壁に加わる力はどの壁においても一様である.
はじめに図1のような,一辺が
の立方体中において速度
で漂う1つの気体分子(質量
)に着目する.
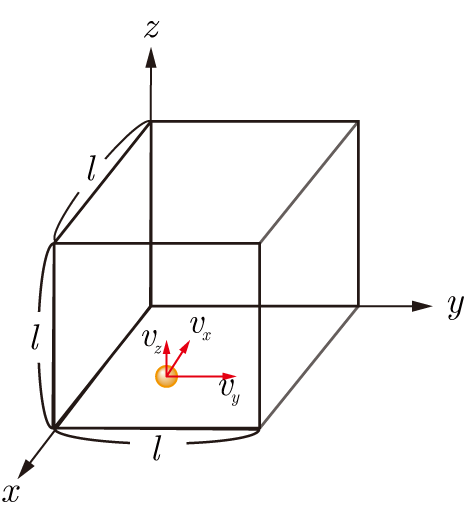
図1:一辺
の立方体中の気体分子
1回の衝突で分子が壁
 に及ぼす力積
に及ぼす力積
図2のように,
軸方向において
の速度成分をもった分子が
軸方向に垂直な壁
に衝突し
の速度成分をもって跳ね返った場合,
軸,
軸方向の速度成分
,
は衝突の前後で変わらない.そのため,分子の運動量は衝突の前後で
だけ変化する.これは壁が分子に及ぼした力積(の
成分)に等しく,作用・反作用の法則により分子が壁に及ぼした力積は
となる.
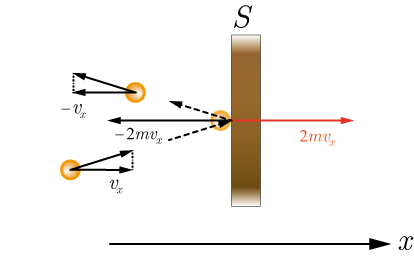
図2:
軸に垂直な面における衝突
1つの分子が単位時間当たり壁
 に及ぼす力積
に及ぼす力積
図3のように,壁
に衝突した分子は、その後別の壁に跳ね返り再び壁
に衝突する.その移動距離は
軸に注目すると,往復で
である.壁
に衝突した分子が往復する時間を
とすると
と表せるので,単位時間あたりに壁
に衝突する回数は
である.よって,1つの分子が単位時間当たりに壁
に及ぼす力積(の
成分)は
となる.
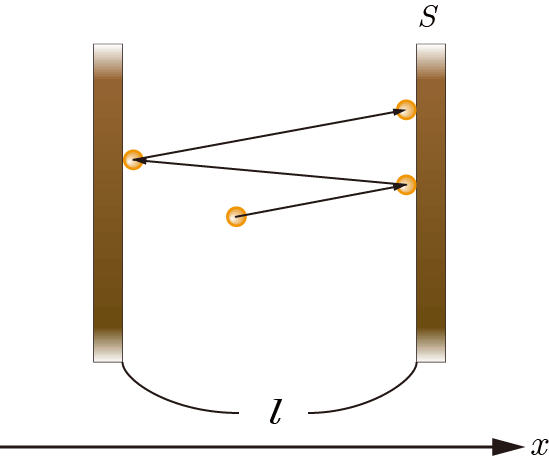
図3:
軸に垂直な面における衝突
 個の分子が壁
個の分子が壁
 に及ぼす力
に及ぼす力
ここで,空間中に漂う
個の分子が壁
に及ぼす力を考える.壁が1つの分子から受ける力の平均を
とすると,単位時間当たりの力積は
と表すことができ,平均の力
は
となる.次に壁
が
個の分子から受けている平均の力の総和
,
個の気体分子についての
の平均を
とすると
であるから,
が
個の分子から受けている平均の力の総和
は
となる(
番目の気体分子の速度の
成分を
,壁
に及ぼす平均の力を
としている).したがって,立方体の容積を
とすると壁
が受ける圧力
は
である.また,図1より
であるため,
個の分子について,その速さの2乗の平均を
,速度成分の2乗の平均をそれぞれ
,
,
とすれば,
である.ここで,立方体の中では多数の分子があらゆる方向に自由に飛び回っているため,気体分子の速度の分布は方向によって変わらない.また,各成分についても方向による違いはないので
である.これらのことから
が得られる.よって気体の圧力は
と表すことができる.
一般に,立方体の容器でなくとも任意の形状の容器(体積
)内の気体の圧力を上式で考えることができる.図4の風船内の気体の圧力も同様である.
図4:風船中の気体分子
学生スタッフ作成
最終更新日: 2025年10月24日