楕円 (ellipse)

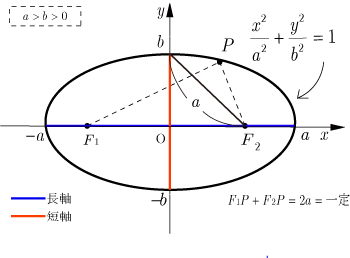
■ 楕円の定義

${\displaystyle {\text{F}}_1{\text{P}+\text{F}}_2\text{P}=}$

一定の長さ　 （ここでは ${\displaystyle 2a}$ とおく）

 を満たす点Pの軌跡のことを楕円という．そして， ${\displaystyle {\text{F}}_1}$ ， ${\displaystyle {\text{F}}_2}$  のことを焦点という．

楕円の方程式（標準形）は

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\left(a>b>0\right)}$

と表される．

焦点 ${\displaystyle {\text{F}}_1}$  の座標： ${\displaystyle \left(-f,0\right)=\left(-\sqrt{a^2-b^2},0\right)}$

焦点 ${\displaystyle {\text{F}}_2}$  の座標： ${\displaystyle \left(f,0\right)=\left(\sqrt{a^2-b^2},0\right)}$

長軸の長さ： ${\displaystyle 2a}$

短軸の長さ： ${\displaystyle 2b}$

 となる．

■ 楕円の方程式の導出

点Pの座標を ${\displaystyle \left(x,y\right)}$  とすると ${\displaystyle {\text{F}}_1{\text{P}+\text{F}}_2\text{P}=2a}$  の関係より

${\displaystyle \sqrt{{\left(x+f\right)}^2+y^2}+\sqrt{{\left(x-f\right)}^2+y^2}=2a}$

${\displaystyle \sqrt{{\left(x+f\right)}^2+y^2}=2a-\sqrt{{\left(x-f\right)}^2+y^2}}$

両辺を2乗して，整理すると

${\displaystyle a\sqrt{{\left(x-f\right)}^2+y^2}=a^2-xf}$

${\displaystyle a^2\left\{{\left(x-f\right)}^2+y^2\right\}=a^4-2a^{2}xf+x^2{f}^2}$

${\displaystyle \left(a^2-f^2\right)x^2+a^2{y}^2=a^2\left(a^2-f^2\right)}$

両辺を ${\displaystyle a^2\left(a^2-f^2\right)}$ で割ると

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{a^2-f^2}=1}$

${\displaystyle b^2+f^2=a^2}$  の関係より

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$

となり，楕円の方程式（基本形）が求まる．

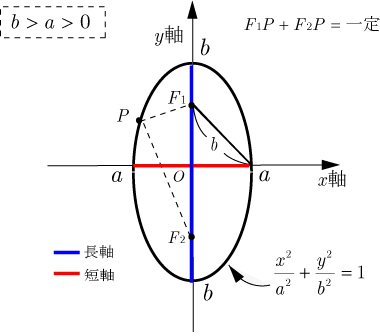
■ 楕円の定義( ${\displaystyle b>a>0}$ の場合)

${\displaystyle a>b>0}$ の場合と違い，焦点が ${\displaystyle y}$ 座標に移る．

焦点 ${\displaystyle F_1}$ の座標： ${\displaystyle \left(0,f\right)=\left(0,\sqrt{b^2-a^2}\right)}$

焦点 ${\displaystyle F_2}$ の座標： ${\displaystyle \left(0,-f\right)=\left(0,-\sqrt{b^2-a^2}\right)}$

長軸の長さ： ${\displaystyle 2b}$

 短軸の長さ： ${\displaystyle 2a}$

となる．

■ 楕円の方程式の導出( ${\displaystyle b>a>0}$ の場合)

点Pの座標を ${\displaystyle \left(x,y\right)}$  とすると ${\displaystyle {\text{F}}_1{\text{P}+\text{F}}_2\text{P}=2b}$  の関係より

${\displaystyle \sqrt{x^2+{\left(y-f\right)}^2}+\sqrt{x^2+{\left(y+f\right)}^2}=2b}$

${\displaystyle \sqrt{x^2+{\left(y+f\right)}^2}=2b-\sqrt{x^2+{\left(y-f\right)}^2}}$

両辺を2乗して，整理すると

${\displaystyle b\sqrt{x^2+{\left(y-f\right)}^2}=b^2-yf}$

${\displaystyle b^2\left\{x^2+{\left(y-f\right)}^2\right\}=b^4-2b^{2}yf+y^2{f}^2}$

${\displaystyle b^2{x}^2+\left(b^2-f^2\right)y^2=b^2\left(b^2-f^2\right)}$

両辺を ${\displaystyle b^2\left(b^2-f^2\right)}$ で割ると

${\displaystyle \frac{x^2}{b^2-f^2}+\frac{y^2}{b^2}=1}$

${\displaystyle a^2+f^2=b^2}$ の関係より

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$

となり，楕円の方程式（基本形）が求まる．

 

ホーム>>カテゴリー分類>>関数>>楕円の方程式

最終更新日 2025年8月24日