x
3
=1
の解
x 3 =1 の解は複素数を学習する上で非常に重要な式です。このページで詳しく解説する。
x 3 =1 の解を求める。
まず, x 3 -1=0 の形にして因数分解する。
( x−1 )( x 2 +x+1 )=0 ・・・・・・(1)
(1)より,
x−1 =0 または, x 2 +x+1=0
x 2 +x+1=0 を解の公式を使って解くと,
x=
−1±
1
2
−4⋅1⋅1
2
=
−1±
−3
2
=
−1±
3
i
2
=−
1
2
±
3
2
i
となり虚数解(ここを参照)となる。
以上より, x 3 =1 の解は
1, − 1 2 + 3 2 ⅈ , − 1 2 - 3 2 ⅈ
となる。
理解をさらに深めるために求まった解を極形式に変えてみる(偏角
θの範囲を 0°<θ<360° とする)。
1=cos0°+sin0°
− 1 2 + 3 2 ⅈ=cos120°+ⅈsin120°
− 1 2 - 3 2 ⅈ=cos240°+ⅈsin240°
となり,複素数の絶対値が1で偏角が0°,120°,240°の120°間隔になっている特徴がある。
x 3 =1 の3つの解を複素平面上に表すと下図のようになる。
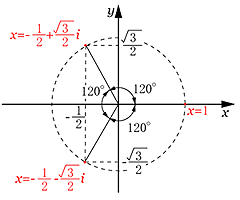
半径1の円上に x=1 を起点として 120°( = 360° 3 )づつ正の方向に
回転したところに解が存在する。
ω=− 1 2 + 3 2 ⅈ とおく( ωを1の原始立方解(虚数立方解)という)と, ω·ω= ω 2 は複素数の積の特徴より複素数 ωを120°回転させた複素数になる。すなはちx 3 =1 の虚数解のもう一方 − 1 2 - 3 2 ⅈ と一致する。
この複素数の積の特徴を利用して,さらにx 3 =1
の解 について考えてみる。
x=1 に − 1 2 + 3 2 ⅈ( =cos120°+ⅈsin120° ) を3回掛けると360°回転して元に戻る。式で表すと,
1
·
(
−
1
2
+
3
2
ⅈ
)
(
−
1
2
+
3
2
ⅈ
)
(
−
1
2
+
3
2
ⅈ
)
=
(
−
1
2
+
3
2
ⅈ
)
3
=
(
cos
120
°
+
ⅈ
sin
120
°
)
3
=
{
cos
(
120
°
×
3
)
+
ⅈ
sin
(
120
°
×
3
)
}
=
cos
360
°
+
ⅈ
sin
360
°
=
1
x=1 に − 1 2 - 3 2 ⅈ( =cos240°+ⅈsin240° ) を3回掛けると720°回転して元に戻る。式で表すと,
1
·
(
−
1
2
−
3
2
ⅈ
)
(
−
1
2
−
3
2
ⅈ
)
(
−
1
2
−
3
2
ⅈ
)
=
(
−
1
2
−
3
2
ⅈ
)
3
=
(
cos
240
°
+
ⅈ
sin
240
°
)
3
=
{
cos
(
240
°
×
3
)
+
ⅈ
sin
(
240
°
×
3
)
}
=
cos
720
°
+
ⅈ
sin
720
°
=
1
このような特徴を一般化したものがド・モアブルの定理であり,
z n =α の解である。
[
り]
[
ら行]
[
索引トップ]

