慣性モーメントの解法の戦略

密度が一様な剛体の慣性モーメントを重積分を用いて計算する場合の解法の戦略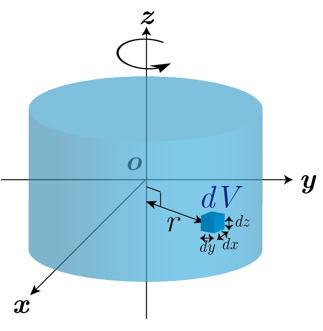

ある回転軸から剛体内の任意の微小領域までの距離が ${\displaystyle r}$ だとするとき， その剛体の慣性モーメント ${\displaystyle I}$ を求める一般式は， 微小質量 ${\displaystyle dm}$ （対象となっている剛体を座標軸ごとに非常に細かく分割した際の任意の一領域 ${\displaystyle dV}$ の質量）を用いて，${\displaystyle I={\displaystyle {\int }_V{r}^2}dm}$ と定義されるが， この式を実際に計算したい物体の形状に当てはめるには幾つか考えておくべきポイントが存在する．

まず初めに，問題となっている物体の次元を把握しよう． 次元によって，用いる式が少し変わってくる．
立体的な形状${\displaystyle \to }$ 三次元，平面的な薄板${\displaystyle \to }$ 二次元，直線的な棒${\displaystyle \to }$ 一次元

(�@)密度を求める
　   三次元では剛体の質量 ${\displaystyle M}$ を体積 ${\displaystyle V}$ で割った密度   ${\displaystyle \rho =\frac{M}{V}}$
　   二次元では剛体の質量 ${\displaystyle M}$ を面積 ${\displaystyle S}$ で割った面密度${\displaystyle \sigma =\frac{M}{S}}$
　   一次元では剛体の質量 ${\displaystyle M}$ を長さ ${\displaystyle L}$ で割った線密度${\displaystyle \lambda =\frac{M}{L}}$ を求めて用いる.

(�A)密度や微小区間を用いて${\displaystyle dm}$を表す
      三次元（${\displaystyle xyz}$ 空間）では微小体積 ${\displaystyle dV=dxdydz}$ を用いれば密度は${\displaystyle \rho =\frac{dm}{dV}}$ でもあるので，
         ${\displaystyle dm=}$ ${\displaystyle \rho }$ ${\displaystyle dV}$ ${\displaystyle =}$ ${\displaystyle \rho }$ ${\displaystyle dxdydz}$
      二次元（${\displaystyle xy}$ 平面）では微小面積  ${\displaystyle dS=dxdy}$   を用いれば面密度は${\displaystyle \sigma =\frac{dm}{dS}}$ でもあるので，
         ${\displaystyle dm=}$ ${\displaystyle \sigma }$ ${\displaystyle dS}$ ${\displaystyle =}$ ${\displaystyle \sigma }$ ${\displaystyle dxdy}$ 　
      一次元（${\displaystyle x}$ 軸）では微小長さ      ${\displaystyle dL=dx}$       を用いれば線密度は${\displaystyle \lambda =\frac{dm}{dL}}$ でもあるので，
         ${\displaystyle dm=}$ ${\displaystyle \lambda }$ ${\displaystyle dL}$ ${\displaystyle =}$ ${\displaystyle \lambda }$ ${\displaystyle dx}$ 　となる.
      ※軸の設定は問題によって異なったり，自分で設定する場合もあるので気を付ける.

(�B)回転軸を把握して，軸からの距離${\displaystyle r}$を座標軸の変数を用いて表す

回転軸からの距離${\displaystyle r}$は，あくまでも（慣性）モーメント なので，回転軸から${\displaystyle dm}$までの最短距離を座標軸の変数（${\displaystyle x,y,z}$ など）を用いて表す． 直交座標系では，質点（点）ではない剛体（連続体）の場合，${\displaystyle r}$は定数とはならない．（極座標系で円環や球殻などを考えるときは，${\displaystyle r}$は半径という定数になる）
※慣性モーメントの式の${\displaystyle r^2}$ が，これまで習った重積分でいうところの被積分関数${\displaystyle f\left(x,y\right)}$ に相当する．

(�C)問題となっている物体の範囲を把握する

物体の形状に応じた変数の取りうる範囲（領域）を把握して，次で式を立てる際に定積分の範囲を入れる．その際，回転軸を基準（あくまでも軸であって点ではないが，原点のこと）として範囲を考える．

(�D)慣性モーメントを求める式を立てる
      三次元（${\displaystyle xyz}$空間）では ${\displaystyle I={\displaystyle {\int }_V{r}^2}dm={\displaystyle \iiint r^2}}$ ${\displaystyle \rho }$ ${\displaystyle dxdydz}$ ${\displaystyle =}$${\displaystyle \frac{M}{V}}$ ${\displaystyle {\displaystyle \iiint r^2}}$${\displaystyle dxdydz}$
      二次元（${\displaystyle xy}$平面）では  ${\displaystyle I={\displaystyle {\int }_V{r}^2}dm=}$  ${\displaystyle {\displaystyle \iint r^2}}$ ${\displaystyle \sigma }$ ${\displaystyle dxdy}$      ${\displaystyle =}$${\displaystyle \frac{M}{S}}$ ${\displaystyle {\displaystyle \iint r^2}}$${\displaystyle dxdy}$
      一次元（${\displaystyle x}$軸）では       ${\displaystyle I={\displaystyle {\int }_V{r}^2}dm=}$    ${\displaystyle {\displaystyle \int r^2}}$ ${\displaystyle \lambda }$ ${\displaystyle dx}$          ${\displaystyle =}$${\displaystyle \frac{M}{L}}$ ${\displaystyle {\displaystyle \int r^2}}$${\displaystyle dx}$

※密度は必ず定数なので，積分の外に予め出しておくと計算ミスを減らせる．
※変数${\displaystyle r}$と積分する変数（つまり軸の変数）が無関係な（つまり定数扱いの）場合，単純に積分範囲の変化量（${\displaystyle a\to b}$ なら${\displaystyle b-a}$ ）を${\displaystyle dm}$に掛けたものを改めて${\displaystyle dm}$と設定することで，累次積分する回数を減らすことができる．演習問題の解説では，この方法を別解として紹介する．

(�E)重積分をする

立式さえできれば，後は${\displaystyle r}$が何の変数なのかを意識しながら重積分を実行すれば，慣性モーメントが求まる．

回転軸について回転対称の物体では，回転軸を原点とした極座標系を用いた方が計算が楽な場合がある． 下記の直交座標系と極座標系の変数の対応式（二次元の場合）${\displaystyle x=r\cos \theta ,y=r\sin \theta ,dxdy=rdrd\theta }$ を思い出して変換しよう．
補足：三次元の場合は，円柱座標系（${\displaystyle r,\theta ,z}$ 軸）だと${\displaystyle dxdydz=rdrd\theta dz}$ となり，極座標系では，${\displaystyle r,\theta }$ に加えてもう一つの角度を表す変数${\displaystyle \varphi }$ を導入した式を使うことになる．

　　　　

[ページトップ]

利用規約

google translate (English version)