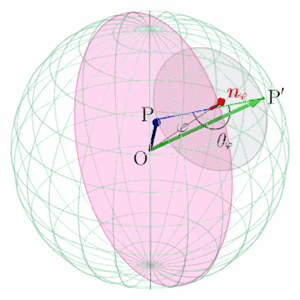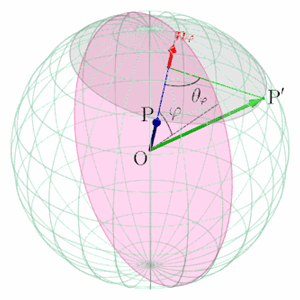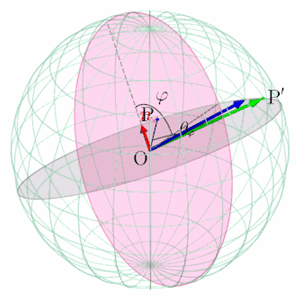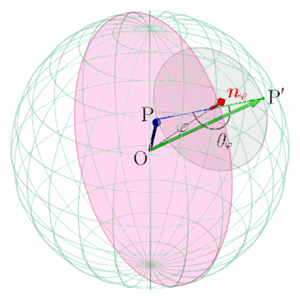
球面上の2点間の移動を表す線形写像 (Linear transformation between 2 points on a sphere)

原点 ${\displaystyle \text{O}}$ を中心とする半径 ${\displaystyle r}$ の球の表面上の異なる2点 ${\displaystyle \text{P}}$ , ${\displaystyle {\text{P}}^{\prime }}$ の間の移動（ 点 ${\displaystyle \text{P}}$ から点 ${\displaystyle {\text{P}}^{\prime }}$ への移動）を表す線形写像 ${\displaystyle f}$ を考える．原点を通り，点 ${\displaystyle \text{P}}$ , ${\displaystyle {\text{P}}^{\prime }}$ からの距離が等しい軸が必ず存在するので，この線形写像はその軸の周りの回転操作に対応づけることができる．

点 ${\displaystyle \text{P}}$ , ${\displaystyle {\text{P}}^{\prime }}$ への位置ベクトルをそれぞれ ${\displaystyle r}$ , ${\displaystyle r^{\prime }}$ とすると，この線形写像はロドリゲスの回転公式を用いて

${\displaystyle r^{\prime }=f_{\phi }(r)}$ ${\displaystyle =r\cos {\theta }_{\phi }+(1-\cos {\theta }_{\phi })(r\cdot n_{\phi })n_{\phi }+(n_{\phi }\times r)\sin {\theta }_{\phi }}$

と表される．ここで， ${\displaystyle n_{\phi }}$ は回転軸方向の単位ベクトル， ${\displaystyle {\theta }_{\phi }}$ は回転角であり，

${\displaystyle n_{\phi }=n_0\cos \phi +(e_n\times n_0)\sin \phi }$     ( ${\displaystyle 0\le \phi \le \pi }$ ) ,
${\displaystyle e_n=\frac{r-r^{\prime }}{\left|r-r^{\prime }\right|}}$  ,   ${\displaystyle n_0=\frac{r+r^{\prime }}{\left|r+r^{\prime }\right|}}$     ( ${\displaystyle r+r^{\prime }\ne 0}$ ) ,
${\displaystyle \cos {\theta }_{\phi }=\frac{r\cdot r^{\prime }-{(r\cdot n_{\phi })}^2}{r^2-{(r\cdot n_{\phi })}^2}}$  ,   ${\displaystyle \sin {\theta }_{\phi }=\sqrt{1-{\cos }^2{\theta }_{\phi }}}$     ( ${\displaystyle 0<{\theta }_{\phi }\le \pi }$ )

で与えられる． ${\displaystyle \phi }$ はパラメータであり， ${\displaystyle 0\le \phi \le \pi }$ の範囲内で任意の値をとる．

${\displaystyle r+r^{\prime }=0}$ （ ${\displaystyle r}$ と ${\displaystyle r^{\prime }}$ が互いに逆向き ）の場合，回転軸方向の単位ベクトル ${\displaystyle n}$ として ${\displaystyle r\cdot n=0}$ を満たすものを考えればよく，回転角 ${\displaystyle \theta }$ は常に ${\displaystyle \theta =\pi }$ である．

---

＜説明＞

点 ${\displaystyle \text{P}}$ から点 ${\displaystyle {\text{P}}^{\prime }}$ への回転移動において，原点を通る回転軸の軸方向の単位ベクトルを ${\displaystyle n}$ とし，点 ${\displaystyle \text{P}}$ , ${\displaystyle {\text{P}}^{\prime }}$ への位置ベクトルをそれぞれ ${\displaystyle r}$ , ${\displaystyle r^{\prime }}$ とする． ${\displaystyle e_n=\frac{r-r^{\prime }}{\left|r-r^{\prime }\right|}}$ を用いると， ${\displaystyle n}$ は

${\displaystyle n\cdot e_n=0}$  ,   ${\displaystyle \left|n\right|=1}$

を満たせばなんでもよい．つまり， ${\displaystyle n}$ は ${\displaystyle e_n}$ を法線ベクトルとする平面上の単位ベクトルであり，その方向には自由度 1 の任意性がある． ${\displaystyle r+r^{\prime }\ne 0}$ の場合，最も簡単な ${\displaystyle n}$ として，

${\displaystyle n_0=\frac{r+r^{\prime }}{\left|r+r^{\prime }\right|}}$

を考える( ${\displaystyle \left|r\right|=\left|r^{\prime }\right|}$ より ${\displaystyle n_0\cdot e_n=0}$ )． ${\displaystyle n_0}$ を基準として回転軸 ${\displaystyle e_n}$ の周りに ${\displaystyle \phi }$ だけ回転したベクトル ${\displaystyle n_{\phi }}$ はロドリゲスの回転公式より

${\displaystyle n_{\phi }=n_0\cos \phi +(1-\cos \phi )(n_0\cdot e_n)e_n+(e_n\times n_0)\sin \phi }$ ${\displaystyle =n_0\cos \phi +(e_n\times n_0)\sin \phi }$

で与えられる．したがって，点 ${\displaystyle \text{P}}$ から ${\displaystyle {\text{P}}^{\prime }}$ への回転移動の回転軸は ${\displaystyle \phi }$ の任意性をもつ単位ベクトル ${\displaystyle n_{\phi }}$ である．

次に，点 ${\displaystyle \text{P}}$ から ${\displaystyle {\text{P}}^{\prime }}$ への回転移動における回転軸 ${\displaystyle n_{\phi }}$ の周りの回転角 ${\displaystyle {\theta }_{\phi }}$ を考える．ここで， ${\displaystyle \phi }$ の範囲を ${\displaystyle 0\le \phi \le \pi }$ に制限すると， ${\displaystyle {\theta }_{\phi }}$ の範囲は ${\displaystyle 0<{\theta }_{\phi }\le \pi }$ に制限される．点 ${\displaystyle \text{P}}$ , ${\displaystyle {\text{P}}^{\prime }}$ を含む回転面の中心を ${\displaystyle {\text{O}}^{\prime }}$ とすると， ${\displaystyle \overrightarrow{\text{O}{\text{O}}^{\prime }}=(r\cdot n_{\phi })n_{\phi }}$ ${\displaystyle =(r^{\prime }\cdot n_{\phi })n_{\phi }}$ であるので，

${\displaystyle \overrightarrow{{\text{O}}^{\prime }\text{P}}=\overrightarrow{\text{O}\text{P}}-\overrightarrow{\text{O}{\text{O}}^{\prime }}}$ ${\displaystyle =r-(r\cdot n_{\phi })n_{\phi }}$
${\displaystyle \overrightarrow{{\text{O}}^{\prime }{\text{P}}^{\prime }}=\overrightarrow{\text{O}{\text{P}}^{\prime }}-\overrightarrow{\text{O}{\text{O}}^{\prime }}}$ ${\displaystyle =r^{\prime }-(r\cdot n_{\phi })n_{\phi }}$

となる．よって，回転半径 ${\displaystyle R_{\phi }}$ は

${\displaystyle R_{\phi }=\left|\overrightarrow{{\text{O}}^{\prime }\text{P}}\right|=\left|\overrightarrow{{\text{O}}^{\prime }{\text{P}}^{\prime }}\right|}$ ${\displaystyle =\left|r-(r\cdot n_{\phi })n_{\phi }\right|}$ ${\displaystyle =\sqrt{{\left\{r-(r\cdot n_{\phi })n_{\phi }\right\}}^2}}$ ${\displaystyle =\sqrt{r^2-{(r\cdot n_{\phi })}^2}}$

である．回転角 ${\displaystyle {\theta }_{\phi }}$ は ${\displaystyle \overrightarrow{{\text{O}}^{\prime }\text{P}}}$ と ${\displaystyle \overrightarrow{{\text{O}}^{\prime }{\text{P}}^{\prime }}}$ との間の角なので，

${\displaystyle \cos {\theta }_{\phi }=\frac{1}{R_{\phi }^2}\left\{r-(r\cdot n_{\phi })n_{\phi }\right\}\cdot \left\{r^{\prime }-(r\cdot n_{\phi })n_{\phi }\right\}}$ ${\displaystyle =\frac{r\cdot r^{\prime }-(r\cdot n_{\phi })(r^{\prime }\cdot n_{\phi })}{r^2-{(r\cdot n_{\phi })}^2}}$ ${\displaystyle =\frac{r\cdot r^{\prime }-{(r\cdot n_{\phi })}^2}{r^2-{(r\cdot n_{\phi })}^2}}$
${\displaystyle \sin {\theta }_{\phi }=\sqrt{1-{\cos }^2{\theta }_{\phi }}}$

が得られる（ ${\displaystyle 0<{\theta }_{\phi }\le \pi }$ より ${\displaystyle \sin {\theta }_{\phi }\ge 0}$ ）．以上より，点 ${\displaystyle \text{P}}$ から点 ${\displaystyle {\text{P}}^{\prime }}$ への移動は，ロドリゲスの回転公式を用いて，点 ${\displaystyle \text{P}}$ の位置ベクトル ${\displaystyle r}$ を回転軸 ${\displaystyle n_{\phi }}$ の周りに角 ${\displaystyle {\theta }_{\phi }}$ だけ回転する線形写像

${\displaystyle r^{\prime }=r\cos {\theta }_{\phi }+(1-\cos {\theta }_{\phi })(r\cdot n_{\phi })n_{\phi }+(n_{\phi }\times r)\sin {\theta }_{\phi }}$

で表すことができる．

${\displaystyle \phi =0}$ のとき， ${\displaystyle n_{\phi }=n_0}$ ${\displaystyle =\frac{r+r^{\prime }}{\left|r+r^{\prime }\right|}}$ であり，

${\displaystyle {(r\cdot n_0)}^2={\left\{\frac{r\cdot (r+r^{\prime })}{\left|r+r^{\prime }\right|}\right\}}^2}$ ${\displaystyle =\frac{{(r^2+r\cdot r^{\prime })}^2}{{(r+r^{\prime })}^2}}$ ${\displaystyle =\frac{r^4+2r^2(r\cdot r^{\prime })+{(r\cdot r^{\prime })}^2}{2r^2+2r\cdot r^{\prime }}}$
${\displaystyle \cos {\theta }_0=\frac{r\cdot r^{\prime }-{(r\cdot n_0)}^2}{r^2-{(r\cdot n_0)}^2}}$ ${\displaystyle =\frac{2r^2(r\cdot r^{\prime })+2{(r\cdot r^{\prime })}^2-\{r^4+2r^2(r\cdot r^{\prime })+{(r\cdot r^{\prime })}^2\}}{2r^4+2r^2(r\cdot r^{\prime })-\{r^4+2r^2(r\cdot r^{\prime })+{(r\cdot r^{\prime })}^2\}}}$ ${\displaystyle =\frac{{(r\cdot r^{\prime })}^2-r^4}{r^4-{(r\cdot r^{\prime })}^2}}$ ${\displaystyle =-1}$

より回転角は ${\displaystyle {\theta }_0=\pi }$ となる（最大の回転角）． ${\displaystyle \phi =\pi /2}$ のとき，

${\displaystyle n_{\pi /2}=n_0\cos \frac{\pi }{2}+(e_n\times n_0)\sin \frac{\pi }{2}}$ ${\displaystyle =e_n\times n_0}$ ${\displaystyle =\frac{(r-r^{\prime })\times (r+r^{\prime })}{\left|r-r^{\prime }\right|\left|r+r^{\prime }\right|}}$ ${\displaystyle =\frac{r\times r^{\prime }}{\sqrt{r^4-{(r\cdot r^{\prime })}^2}}}$

であり， ${\displaystyle r\cdot (r\times r^{\prime })=0}$ より ${\displaystyle r\cdot n_{\pi /2}=0}$ なので， ${\displaystyle \cos {\theta }_{\pi /2}=\frac{r\cdot r^{\prime }}{r^2}}$ となる．このときの ${\displaystyle {\theta }_{\pi /2}}$ が最小の回転角となる．また， ${\displaystyle \phi =\pi }$ のとき ${\displaystyle n_{\pi }=-n_0}$ なので， ${\displaystyle \phi =0}$ のときと同様に ${\displaystyle \cos {\theta }_{\pi }=-1}$ より ${\displaystyle {\theta }_{\pi }=\pi }$ となる．

ホーム>>カテゴリー分類>>物理数学>>線形代数>>球面上の2点間の移動を表す線形写像