円の接線の方程式 

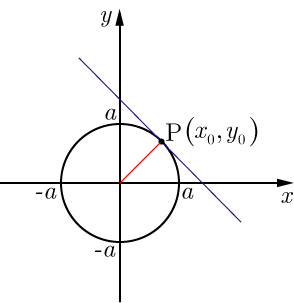原点を中心とする半径 a の円周上の点P${\displaystyle \left(x_0,y_0\right)}$における接線の方程式は

${\displaystyle x_{0}x+y_{0}y=a^2}$

である．

■導出計算

円の方程式は

${\displaystyle x^2+y^2=a^2}$  

である．この両辺をx で微分すると

${\displaystyle 2x+2y\frac{dy}{dx}=0}$  

となり，${\displaystyle \frac{dy}{dx}}$ について整理すると

${\displaystyle \frac{dy}{dx}=-\frac{x}{y}}$  

よって，P点での傾きは，${\displaystyle -\frac{x_0}{y_0}}$となる． 以上より，点Pにおける接線の方程式は

${\displaystyle y-y_0=-\frac{x_0}{y_0}\left(x-x_0\right)}$  

となる．この接線の方程式を更に以下のように変形する．

まず，両辺に ${\displaystyle y_0}$ を掛けて，

${\displaystyle y_0\left(y-y_0\right)=-x_0\left(x-x_0\right)}$  

${\displaystyle x_{0}x+y_{0}y={x_0}^2+{y_0}^2}$  

${\displaystyle {x_0}^2+{y_0}^2=a^2}$  より，

${\displaystyle x_{0}x+y_{0}y=a^2}$  

となり，上で示した接線の方程式が得られた．

ホーム>>カテゴリー分類>>微分>>接線の方程式>>円の接線の方程式

最終更新日： 2023年5月30日