中間値の定理
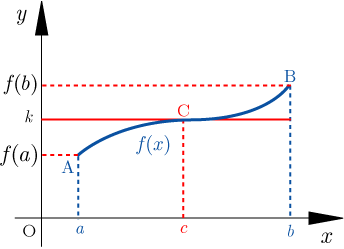 関数 が閉区間 で連続,かつ ならば, との中間の値
に対して
関数 が閉区間 で連続,かつ ならば, との中間の値
に対して
()
を満たすような が存在する.
■証明
●の場合
関数の での連続性の定義は,「任意の正の実数 に対して,適当な正の数があって,のすべてのについて となる」と表わされる.ここで, ,,, として定義を適用すると ,ある区間 の任意の 注1) において,常に 注2) となる が存在し,その集合を とする. (ただし, )より,には上限がある.その上限の値を とすると, となる.
注1) , より, , , よって,
注2) の場合: , ,よって,
の場合: , より,
とすると,十分小さい に対して, となってしまい, が上限であることに矛盾する.また, とすると,十分小さい に対して, となってしまい, が上限であることに矛盾する.したがって,となるが集合の上限の値で, より ,となる.以上より, は の1つである.
の場合も同様である.
最終更新日: 2024年5月28日