特定の範囲に解をもつための2次方程式の条件
2次方程式 がの範囲で解をもつための条件について考える.
まず, とおく.
■ の範囲で解を1つもつ場合
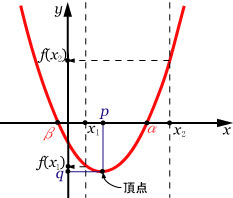 (1)右図参照:右の図は の係数 が正の場合のグラフであるが, が負の場合も同じように考えることができる. |
■ の範囲で解を2つもつ場合
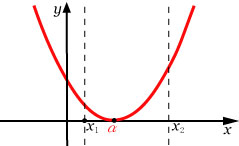 (2) (重解をもつ場合)
|
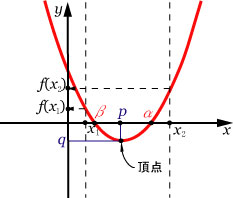 (1) の場合, (についてはここを参照 ) |
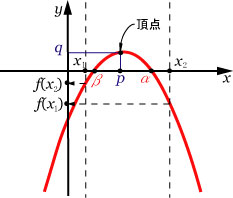 (2) の場合, (についてはここを参照 ) |
ホーム>>カテゴリー分類>>関数>>特定の範囲に解をもつための関数の条件
最終更新日: 2023年7月27日