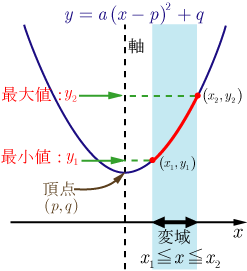
の範囲に指定がある場合の2次関数の最大・最小
2次関数 について考える.
の指定範囲(変域) と頂点の 座標(軸)の位置関係に注意して最大値,最小値を求める.その場合, が正,負においてそれそれ以下に示す5つの場合が考えられる.
■ の場合
(右図参照,変域は とする.)
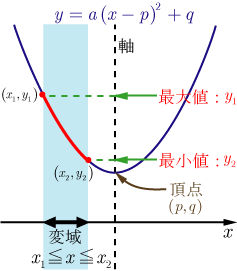
● の場合で最大, で最小となる. |
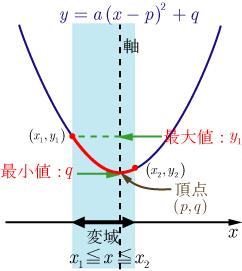
● かつ の場合で最大, で最小となる. |
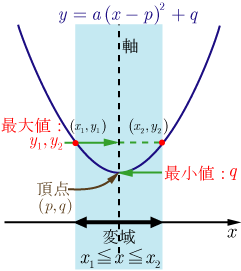
● の場合, で最大, で最小となる. |
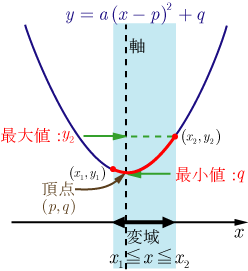
● かつ の場合で最大, で最小となる. |
● の場合で最大, で最小となる. |
■ の場合
グラフが上下対称になるので, の場合における最小値と最大値が入れ替わる.確かめて見よう.
ホーム>>カテゴリー分類>>関数>>2次関数の最大と最小(範囲指定あり)
最終更新日: 2025年2月14日