双曲線 (hyperbola)

目次

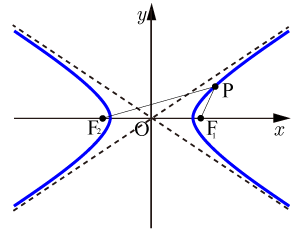
1. 双曲線の定義 (焦点がx軸上の場合)
2. 双曲線の方程式 (焦点がx軸上の場合)
3. 双曲線の方程式の漸近線 (焦点がx軸上の場合)
4. 双曲線の定義 (焦点がy軸上の場合)
5. 双曲線の方程式 (焦点がy軸上の場合)
6. 双曲線の方程式の漸近線 (焦点がy軸上の場合)

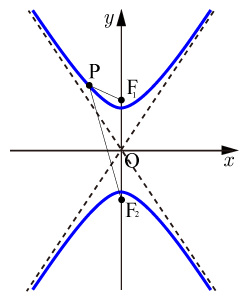
■双曲線の定義(焦点がx軸上の場合)

平面上で，${\displaystyle 2}$ 定点 ${\displaystyle F_1}$ ， ${\displaystyle F_2}$  からの距離の差が一定で点の軌跡を双曲線といい

点 ${\displaystyle F_1}$ ， ${\displaystyle F_2}$  を焦点という．

${\displaystyle c>0}$ のとき，焦点座標は ${\displaystyle F_1\left(c,0\right)}$ ， ${\displaystyle F_2\left(-c,0\right)}$ である．

${\displaystyle P\left(x,y\right)}$ であるから

${\displaystyle F_{1}P=\sqrt{{\left|x-c\right|}^2+{\left|y\right|}^2}}$ ，${\displaystyle F_{2}P=\sqrt{{\left|x-\left(-c\right)\right|}^2+{\left|y\right|}^2}}$

${\displaystyle \left|F_{1}P-F_{2}P\right|=2a}$  ${\displaystyle \left(c>a\right)}$ となる．

${\displaystyle 2a}$  は双曲線の${\displaystyle x}$  軸との交点の距離の差である．

${\displaystyle 2a=a-(-a)}$

より，双曲線の${\displaystyle x}$  軸との交点の${\displaystyle x}$  座標の値は${\displaystyle a}$ ， ${\displaystyle -a}$ である．

この双曲線を表す方程式は

${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}$ 　(ただし，${\displaystyle b=\sqrt{c^2-a^2}}$ )

となる．

ページトップへ

■双曲線の方程式 ${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}$  の導出(焦点がx軸上の場合)

◆${\displaystyle F_{2}P>F_{1}P}$ の時

両辺を${\displaystyle 2}$ 乗して，整理すると

${\displaystyle 2cx=4a^2+4a\sqrt{{\left(x-c\right)}^2+y^2}-2cx}$

${\displaystyle 4a\sqrt{{\left(x-c\right)}^2+y^2}=4cx-4a^2}$

${\displaystyle \sqrt{{\left(x-c\right)}^2+y^2}=\frac{c}{a}x-a}$

更に両辺を${\displaystyle 2}$ 乗する．

${\displaystyle {\left(x-c\right)}^2+y^2={\left(\frac{c}{a}x-a\right)}^2}$

${\displaystyle x^2+c^2+y^2=\frac{c^2}{a^2}{x}^2+a^2}$

${\displaystyle \left(1-\frac{c^2}{a^2}\right)x^2+y^2=a^2-c^2}$

${\displaystyle \frac{a^2-c^2}{a^2}{x}^2+y^2=a^2-c^2}$

両辺を ${\displaystyle a^2-c^2}$ で割る．

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1}$

${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{c^2-a^2}=1}$

${\displaystyle c>a}$  より ${\displaystyle c^2-a^2>0}$となる．よって${\displaystyle c^2-a^2=b^2}$，${\displaystyle b>0}$ とおくと

${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}$

となる．

◆${\displaystyle F_{1}P>F_{2}P}$ のとき

両辺を2乗する．

左辺と右辺を整理して

${\displaystyle -2cx=4a^2+4a\sqrt{{\left(x+c\right)}^2+y^2}+2cx}$

${\displaystyle 4a\sqrt{{\left(x+c\right)}^2+y^2}=-4cx-4a^2}$

${\displaystyle \sqrt{{\left(x+c\right)}^2+y^2}=-\frac{c}{a}x-a}$

更に両辺を2乗する．

${\displaystyle {\left(x+c\right)}^2+y^2={\left(-\frac{c}{a}x-a\right)}^2}$

${\displaystyle x^2+2cx+c^2+y^2}$${\displaystyle =\frac{c^2}{a^2}{x}^2+2cx+a^2}$

${\displaystyle x^2+c^2+y^2=\frac{c^2}{a^2}{x}^2+a^2}$

${\displaystyle \left(1-\frac{a^2}{c^2}\right)x^2+y^2=a^2-c^2}$

${\displaystyle \frac{a^2-c^2}{a^2}{x}^2+y^2=a^2-c^2}$

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{a^2-c^2}=1}$

${\displaystyle \frac{x^2}{a^2}+\frac{y^2}{-\left(c^2-a^2\right)}=1}$

${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{c^2-a^2}=1}$

${\displaystyle c>a}$  より ${\displaystyle c^2-a^2>0}$となる．よって${\displaystyle c^2-a^2=b^2}$，${\displaystyle b>0}$ とおくと

${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}$

となる．

このように， ${\displaystyle F_{2}P>F_{1}P}$  のときと， ${\displaystyle F_{1}P>F_{2}P}$ のときで，双曲線の方程式が等しくなる．

ページトップへ

■双曲線の方程式 ${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}$  の漸近線(焦点がx軸上の場合)

双曲線の方程式 ${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}$  より

${\displaystyle \frac{y^2}{b^2}=\frac{x^2}{a^2}-1}$

${\displaystyle y^2=\frac{b^2}{a^2}{x}^2-b^2}$

${\displaystyle y^2=\frac{b^2}{a^2}{x}^2\left(1-\frac{a^2}{x^2}\right)}$

${\displaystyle y=\pm \frac{b}{a}x\sqrt{1-\frac{a^2}{x^2}}}$

${\displaystyle x\to \infty }$  あるいは， ${\displaystyle x\to -\infty }$  の時，${\displaystyle \frac{a^2}{x^2}\to 0}$  に近づく．

したがって， ${\displaystyle y=\pm \frac{b}{a}x\sqrt{1-0}}$より，${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=1}$ の漸近線は

${\displaystyle y=\pm \frac{b}{a}x}$  

となる．

ページトップへ

■双曲線の定義(焦点がy軸上の場合)

${\displaystyle F_1\left(0,c\right)}$

${\displaystyle F_2\left(0,-c\right)}$

${\displaystyle F_{1}P=\sqrt{{\left|x\right|}^2+{\left|y-c\right|}^2}}$

${\displaystyle F_{2}P=\sqrt{{\left|x\right|}^2+{\left|y-\left(-c\right)\right|}^2}}$

${\displaystyle \left|F_{1}P-F_{2}P\right|=2b}$

${\displaystyle c>b}$

距離の差 ${\displaystyle 2b}$

双曲線の${\displaystyle y}$ 軸との交点の${\displaystyle y}$ 座標の値は${\displaystyle b,-b}$

この双曲線を表す方程式は

${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1}$ 　(ただし，${\displaystyle a=\sqrt{c^2-b^2}}$ )

となる．

ページトップへ

■双曲線の方程式 ${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1}$  の導出(焦点がy軸上の場合)

◆${\displaystyle F_{2}P>F_{1}P}$ の時

${\displaystyle 4b\sqrt{x^2+{\left(y-c\right)}^2}=4cy-4b^2}$

${\displaystyle \sqrt{x^2+{\left(y-c\right)}^2}=\frac{c}{b}y-b}$

${\displaystyle x^2+{\left(y-c\right)}^2={\left(\frac{c}{b}y-b\right)}^2}$

${\displaystyle x^2+y^2-2cy+c^2=\frac{c^2}{b^2}{y}^2-2cy+b^2}$

${\displaystyle x^2+\left(1-\frac{c^2}{b^2}\right)y^2=b^2-c^2}$

${\displaystyle x^2+\frac{b^2-c^2}{b^2}{y}^2=b^2-c^2}$

${\displaystyle \frac{x^2}{b^2-c^2}+\frac{y^2}{b^2}=1}$

${\displaystyle \frac{x^2}{-\left(c^2-b^2\right)}+\frac{y^2}{b^2}=1}$

${\displaystyle c>b}$  より ${\displaystyle c^2-b^2>0}$となる．よって${\displaystyle c^2-b^2=a^2}$，${\displaystyle a>0}$ とおくと ${\displaystyle c^2-b^2=a^2}$  とおくと

${\displaystyle -\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$

${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1}$

となる．

◆${\displaystyle F_{1}P>F_{2}P}$  の時

${\displaystyle 4b\sqrt{x^2+{\left(y+c\right)}^2}}$${\displaystyle =-4cy-4b^2}$

${\displaystyle \sqrt{x^2+{\left(y+c\right)}^2}}$${\displaystyle =-\frac{c}{b}y-b}$

${\displaystyle x^2+{\left(y+c\right)}^2={\left(-\frac{c}{b}y-b\right)}^2}$

${\displaystyle x^2+y^2+2cy+c^2}$${\displaystyle =\frac{c^2}{b^2}{y}^2+2cy+b^2}$

${\displaystyle x^2+\left(1-\frac{c^2}{b^2}\right)y^2=b^2-c^2}$

${\displaystyle x^2+\frac{b^2-c^2}{b^2}{y}^2=b^2-c^2}$

${\displaystyle \frac{x^2}{b^2-c^2}+\frac{y^2}{b^2}=1}$

${\displaystyle \frac{x^2}{-\left(c^2-b^2\right)}+\frac{y^2}{b^2}=1}$

${\displaystyle -\frac{x^2}{c^2-b^2}+\frac{y^2}{b^2}=1}$

${\displaystyle c>b}$  より ${\displaystyle c^2-b^2>0}$となる．よって${\displaystyle c^2-b^2=a^2}$，${\displaystyle a>0}$ とおくと ${\displaystyle c^2-b^2=a^2}$  とおくと

${\displaystyle -\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$

両辺に${\displaystyle -1}$ を掛けて

${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1}$

となる．

このように， ${\displaystyle F_{2}P>F_{1}P}$ の場合と${\displaystyle F_{1}P>F_{2}P}$ の場合で方程式が等しくなる．

ページトップへ

■双曲線の方程式${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1}$ の漸近線(焦点がy軸上の場合)

${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1}$より

${\displaystyle \frac{y^2}{b^2}=\frac{x^2}{a^2}+1}$

${\displaystyle y^2=\frac{b^2}{a^2}{x}^2+b^2}$

${\displaystyle y^2=\frac{b^2}{a^2}{x}^2\left(1+\frac{a^2}{x^2}\right)}$

${\displaystyle y=\pm \frac{b}{a}x\sqrt{1+\frac{a^2}{x^2}}}$

${\displaystyle x\to \infty }$  あるいは，${\displaystyle x\to -\infty }$  の時，${\displaystyle \frac{a^2}{x^2}\to 0}$ となるので，${\displaystyle y}$  の値は${\displaystyle \pm \frac{b}{a}x}$ に近づく．

すなわち，${\displaystyle \frac{x^2}{a^2}-\frac{y^2}{b^2}=-1}$ のグラフの漸近線は

${\displaystyle y=\pm \frac{b}{a}x}$

となる．

ページトップへ

ホーム>>カテゴリー分類>>関数>>双曲線の方程式

学生スタッフ作成

最終更新日： 2024年7月24日