相似条件

相似とは，同じ形の図形のことをいう．相似の記号は∽で表す．

■三角形の相似条件

●3組の辺の比が等しい

　

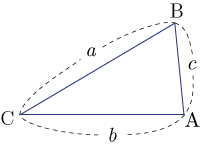
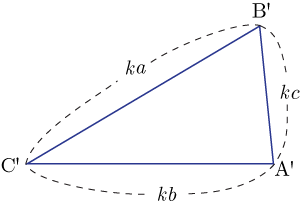
相似に対応する辺の比が等しい．よって

${\displaystyle \frac{{\text{A}}^{\prime }{\text{B}}^{\prime }}{\text{AB}}=\frac{{\text{B}}^{\prime }{\text{C}}^{\prime }}{\text{BC}}=\frac{{\text{A}}^{\prime }{\text{C}}^{\prime }}{\text{AC}}=k}$

となる．

●2組の辺の比が等しく，その間の角が等しい

　

　　　　 　　　　　　　　　　

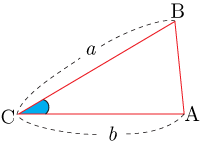
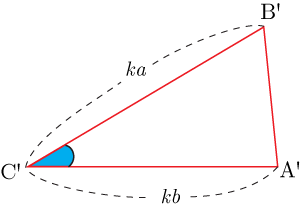
●2角の角がそれぞれ等しい

　

■相似な平面図形の面積比

相似な三角形で，対応する部分の長さが${\displaystyle k}$ 倍なら，面積は${\displaystyle k^2}$倍である．⇒証明

　

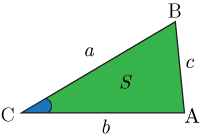
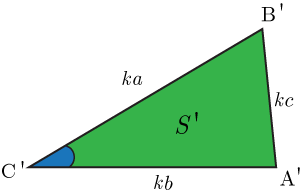
上の図三角形${\displaystyle \text{ABC}}$ の面積を${\displaystyle S1}$ ，三角形$A^{\prime }{B}^{\prime }{C}^{\prime }$の面積を${\displaystyle S2}$とすると，${\displaystyle S:S^{\prime }=1:k^2}$ となる．

■相似な立体の表面積比

相似な立体で，対応する部分の長さが${\displaystyle k}$ 倍なら，表面積は${\displaystyle k^2}$倍である．⇒証明

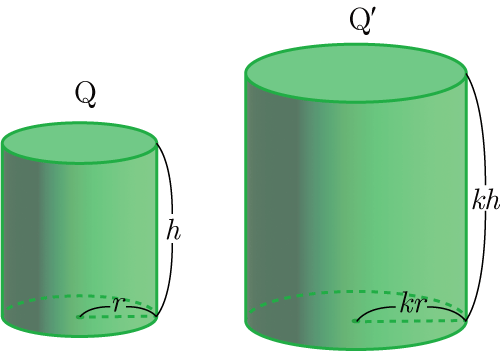
上の図の場合，$\text{Q}$ と ${\text{Q}}^{\prime }$は相似比が${\displaystyle 1:k}$であると，表面積比は${\displaystyle 1:k^2}$ となる．

■相似な立体の体積比

相似な立体で対応する部分の長さが${\displaystyle k}$ 倍なら，体積は${\displaystyle k^3}$倍である．⇒証明

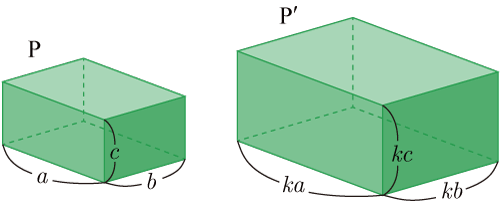
上の図の場合，$\text{P}$ と ${\text{P}}^{\prime }$ は相似比が ${\displaystyle 1:k}$  であると，体積比は${\displaystyle 1:k^3}$ となる．

 

ホーム>>カテゴリー分類>>幾何>>相似条件

最終更新日： 2026年10月6日