最小二乗法

ある物理量 $y$ がある物理量 $x$ の関数で

$y = a x + b$

と表されるとする．例えば $x$ の値を決めて $y$ の値を測定する作業を $n$ 回繰り返し，表のように $n$ 個の $x$ と $y$ の対が得られたとする．

測定回数	$1$	$2$	$3$	……	$n - 1$	$n$
$x$ の値	$x_{1}$	$x_{2}$	$x_{3}$	……	$x_{n - 1}$	$x_{n}$
$y$ の値	$y_{1}$	$y_{2}$	$y_{3}$	……	$y_{n - 1}$	$y_{n}$

この $x$ と $y$ の対を $x y$ 座標上にプロットすると

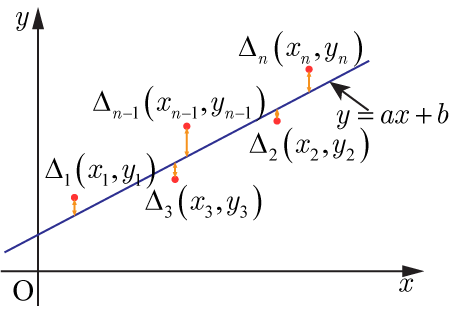
となり，実験条件のバラツキや測定誤差などの要因で，プロットした点は直線上に乗らない．(本来なら $y = a x + b$ の関係があるので，すべての点は直線上に乗るはずである．)

プロットした点と $y = a x + b$ との $y$ 軸方向の値の差 $Δ_{i}$ は

$Δ_{i} = y_{i} - (a x_{i} + b)$

となる． $a$ ， $b$ の値によって $Δ_{i}$ の値は変化する．すべての点で $Δ_{i}$ の値を小さくする $a$ ， $b$ の値が， $x$ と $y$ の関係を表す最も確からしい値だと考えることができる． $a$ ， $b$ の値を決める方法として

$Δ^{2} = \sum_{i = 1}^{n} Δ i^{2} = \sum_{i = 1}^{n} {y_{i} - (a x_{i} + b)}^{2}$

の値を最小とする $a$ ， $b$ を用いる方法がある．この方法のことを最小二乗法という．

● $Δ^{2}$ は最小となる $a$ と $b$ の値

$a = \frac{σ_{x y}}{σ_{x}^{2}}$ ， $b = \bar{y} - a \bar{x}$

ただし

$\bar{x} = \frac{1}{n} \sum_{i = 1}^{n} x_{i}$ ， $\bar{y} = \frac{1}{n} \sum_{i = 1}^{n} y_{i}$ (参照：平均)

$σ_{x y} = \frac{1}{n} \sum_{i = 1}^{n} x_{i} y_{i} - \bar{x} \bar{y}$ (参照：共分散)

$σ_{x}^{2} = \frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} - {\bar{x}}^{2}$ (参照：分散)

■導出

偏導関数を用いた計算 ⇒ ここ

$Δ^{2}$ の最小となる $a$ ， $b$ の値を平方完成を利用して求める．

$Δ^{2} = \sum_{i = 1}^{n} {y_{i} - (a x_{i} + b)}^{2}$

$= \sum_{i = 1}^{n} {y_{i}^{2} - 2 (a x_{i} + b) y_{i} + {(a x_{i} + b)}^{2}}$

$= \sum_{i = 1}^{n} {y_{i}^{2} - 2 a x_{i} y_{i} - 2 b y_{i} + a^{2} x_{i}^{2} + 2 a b x_{i} + b^{2}}$

$= \sum_{i = 1}^{n} y_{i}^{2} + \sum_{i = 1}^{n} (- 2 a x_{i} y_{i}) + \sum_{i = 1}^{n} (- 2 b y_{i})$ $+ \sum_{i = 1}^{n} a^{2} x_{i}^{2}$ $+ \sum_{i = 1}^{n} 2 a b x_{i}$ $+ \sum_{i = 1}^{n} b^{2}$

$= \sum_{i = 1}^{n} y_{i}^{2} - 2 a \sum_{i = 1}^{n} x_{i} y_{i} - 2 b \sum_{i = 1}^{n} y_{i}$ $+ a^{2} \sum_{i = 1}^{n} x_{i}^{2}$ $+ 2 a b \sum_{i = 1}^{n} x_{i}$ $+ n b^{2}$

$\sum_{i = 1}^{n} y_{i}^{2} = A$ ， $\sum_{i = 1}^{n} x_{i} y_{i} = B$ ， $\sum_{i = 1}^{n} y_{i} = C$ ， $\sum_{i = 1}^{n} x_{i}^{2} = D$ ， $\sum_{i = 1}^{n} x_{i} = E$ とおくと

$= A - 2 a B - 2 b C + a^{2} D + 2 a b E + n b^{2}$

$= n b^{2} + 2 (E a - C) b + D a^{2} - 2 B a + A$

$= n {(b + \frac{E a - C}{n})}^{2} - \frac{1}{n} {(E a - C)}^{2}$ $+ D a^{2}$ $- 2 B a + A$

$= n {(b + \frac{E a - C}{n})}^{2}$ $+ \frac{1}{n} (- E^{2} a^{2} + 2 C E a - C^{2} + n D a^{2} - 2 n B a + n A)$

$= n {(b + \frac{E a - C}{n})}^{2}$ $+ \frac{1}{n} \{(n D - E^{2}) a^{2} + 2 (C E - n B) a + n A - C^{2}\}$

$= n {(b + \frac{E a - C}{n})}^{2}$ $+ \frac{1}{n} (n D - E^{2}) {(a + \frac{C E - n B}{n D - E^{2}})}^{2}$ $- \frac{1}{n} \frac{{(C E - n B)}^{2}}{n D - E^{2}} + A - \frac{1}{n} C^{2}$

これより， $Δ^{2}$ が最小になるのは

$b + \frac{E a - C}{n} = 0$ ， $a + \frac{C E - n B}{n D - E^{2}} = 0$

の時である．よって

$a$ $= - \frac{C E - n B}{n D - E^{2}}$

$= \frac{n B - C E}{n D - E^{2}}$

$= \frac{\frac{1}{n^{2}} \{n \sum_{i = 1}^{n} x_{i} y_{i} - \sum_{i = 1}^{n} x_{i} \sum_{i = 1}^{n} y_{i}\}}{\frac{1}{n^{2}} \{n \sum_{i = 1}^{n} x_{i}^{2} - {(\sum_{i = 1}^{n} x_{i})}^{2}\}}$

$= \frac{\frac{1}{n} \sum_{i = 1}^{n} x_{i} y_{i} - (\frac{1}{n} \sum_{i = 1}^{n} x_{i}) (\frac{1}{n} \sum_{i = 1}^{n} y_{i})}{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} - {(\frac{1}{n} \sum_{i = 1}^{n} x_{i})}^{2}}$

ここで

$\bar{x} = \frac{1}{n} \sum_{i = 1}^{n} x_{i}$ ， $\bar{y} = \frac{1}{n} \sum_{i = 1}^{n} y_{i}$ (参照：平均)　･･････(1)

$σ_{x y} = \frac{1}{n} \sum_{i = 1}^{n} x_{i} y_{i} - \bar{x} \bar{y}$ (参照：共分散)　･･････(2)

$σ_{x}^{2} = \frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} - {\bar{x}}^{2}$ (参照：分散)　･･････(3)

とおくと

$= \frac{σ_{x y}}{σ_{x}^{2}}$ ･･････(4)

$b$ $= - \frac{E a - C}{n}$

$= \frac{C - E a}{n}$

$= \frac{1}{n} (C - E \frac{n B - C E}{n D - E^{2}})$

$= \frac{1}{n} \frac{n C D - C E^{2} - n B E + C E^{2}}{n D - E^{2}}$

$= \frac{C D - B E}{n D - E^{2}}$

$= \frac{\sum_{i = 1}^{n} x_{i}^{2} \sum_{i = 1}^{n} y_{i} - \sum_{i = 1}^{n} x_{i} y_{i} \sum_{i = 1}^{n} x_{i}}{n \sum_{i = 1}^{n} x_{i}^{2} - {(\sum_{i = 1}^{n} x_{i})}^{2}}$

$= \frac{\frac{1}{n^{2}} (\sum_{i = 1}^{n} x_{i}^{2} \sum_{i = 1}^{n} y_{i} - \sum_{i = 1}^{n} x_{i} y_{i} \sum_{i = 1}^{n} x_{i})}{\frac{1}{n^{2}} \{n \sum_{i = 1}^{n} x_{i}^{2} - {(\sum_{i = 1}^{n} x_{i})}^{2}\}}$

$= \frac{(\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2}) (\frac{1}{n} \sum_{i = 1}^{n} y_{i}) - (\frac{1}{n} \sum_{i = 1}^{n} x_{i} y_{i}) (\frac{1}{n} \sum_{i = 1}^{n} x_{i})}{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} - {(\frac{1}{n} \sum_{i = 1}^{n} x_{i})}^{2}}$

(1)より

$= \frac{(\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2}) \bar{y} - (\frac{1}{n} \sum_{i = 1}^{n} x_{i} y_{i}) \bar{x}}{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} - {\bar{x}}^{2}}$

$= \frac{(\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2}) \bar{y} - {\bar{x}}^{2} \bar{y} + {\bar{x}}^{2} \bar{y} - (\frac{1}{n} \sum_{i = 1}^{n} x_{i} y_{i}) \bar{x}}{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} - {\bar{x}}^{2}}$

$= \frac{\{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} - {\bar{x}}^{2}\} \bar{y} - \bar{x} \{\frac{1}{n} \sum_{i = 1}^{n} x_{i} y_{i} - \bar{x} \bar{y}\}}{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} - {\bar{x}}^{2}}$

$= \bar{y} - \frac{\frac{1}{n} \sum_{i = 1}^{n} x_{i} y_{i} - \bar{x} \bar{y}}{\frac{1}{n} \sum_{i = 1}^{n} x_{i}^{2} - {\bar{x}}^{2}} \bar{x}$

(2)，(3)より

$= \bar{y} - \frac{σ_{x y}}{σ_{x}^{2}} \bar{x}$

(4)より

$= \bar{y} - a \bar{x}$

以上をまとめると

$a = \frac{σ_{x y}}{σ_{x}^{2}}$ ， $b = \bar{y} - a \bar{x}$

とき $Δ^{2}$ は最小となる．

ホーム>>カテゴリー別分類>>その他>>最小二乗法

最終更新日 2026年4月20日

最小二乗法

● Δ 2 は最小となる a と b の値

■導出

● $Δ^{2}$ は最小となる $a$ と $b$ の値