和積の公式
-
⇒公式の導出
-
⇒公式の導出
-
⇒公式の導出
-
⇒公式の導出
■公式の導出
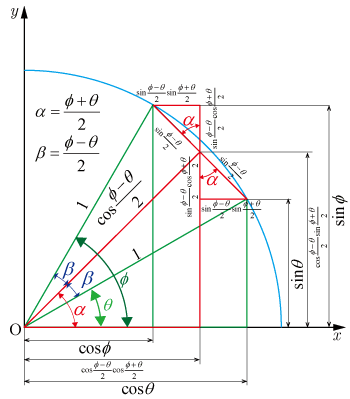 ●
の公式の導出
●
の公式の導出
積和の公式
に,
,
として代入すると
したがって
となる.
●
の公式の導出
積和の公式
に,
,
として代入すると
したがって
となる.
●
の公式の導出
積和の公式
に,
,
として代入すると
したがって
となる.
●
の公式の導出
積和の公式
に,
,
として代入すると
したがって
となる.
ホーム>>カテゴリー分類>>三角関数>>和積の公式
最終更新日:
2026年2月10日
 ●
の公式の導出
●
の公式の導出