弧度法の定義
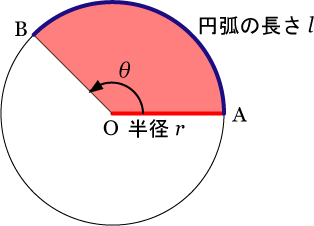 右図のような扇型OABを考える.中心角
は円弧の長さ
に比例する.円弧の長さ
と扇型の半径
の比をとると,同じ角度
に対して扇型の大きさにかかわらずこの比は一定である.この性質を利用して角度の大きさを定めたのが弧度法で
右図のような扇型OABを考える.中心角
は円弧の長さ
に比例する.円弧の長さ
と扇型の半径
の比をとると,同じ角度
に対して扇型の大きさにかかわらずこの比は一定である.この性質を利用して角度の大きさを定めたのが弧度法で
・・・・・・(1)
とする.単位はラジアン(rad)で,通常単位名のラジアンは省略する.この弧度法に対して,45°,60°と表現する方法を度数法という.
弧度法を用いると,(1)より円弧の長さ は
(円弧の長さ=半径×中心角) ・・・・・・(2)
となり,とても簡単な式になる.
半径 のとき
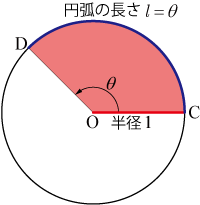
(1)より
(単位円の円弧の長さ=中心角) ・・・・・・(3)
となる.このことより弧度法を用いると
が導かれる.この関係より の微分が となり,三角関数の微分,積分が単純になる.
■度数法と弧度法の対比
-
度数法(単位:deg,度,°) 弧度法(単位:rad,ラジアン) -
0° 0 -
30° -
45° -
60° -
90° -
180° -
270° -
360°
参考:円周の長さ=直径× (円周率)であるが,このことより度数法による360°が2 に対応する.
●度数法から弧度法に変換する式
弧度法の角度 度数法の角度
●弧度法から度数法に変換する式
度数法の角度 弧度法の角度
最終更新日: 2025年4月25日