指数関数 0<a<1

■指数関数の性質 (${\displaystyle 0<a<1}$ の場合)

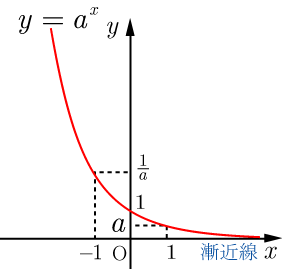
${\displaystyle x}$の値が増加すれば，${\displaystyle y}$の値は減少する単調減少である．(単調減少関数)

すなわち，


${\displaystyle x}$の値が増加すると，グラフは${\displaystyle x}$軸に限りなく近づく．(${\displaystyle x}$軸が漸近線) 　

定義域：実数全体，　値域：正の数全体，　グラフ：点${\displaystyle \left(0,1\right)}$を通る．

(${\displaystyle y=a^x}$は単調増加するので，${\displaystyle x}$ と${\displaystyle y}$ は1対1の関係によるものである．)

${\displaystyle y=a^x}$と${\displaystyle y={\left(\frac{1}{a}\right)}^x}$すなわち，${\displaystyle y=a^x}$と${\displaystyle y=a^{-x}}$は${\displaystyle x}$軸に対して対称である．

具体的な指数関数のグラフ例 ⇒ ココ　　　指数関数の性質(${\displaystyle a>1}$) ⇒ ココ

 

ホーム>>カテゴリー別分類>>指数/対数>>指数関数>>指数関数の性質 (${\displaystyle 0<a<1}$)

最終更新日： 2023年7月28日