たすきがけ手法による因数分解の手順

2次関数 ${\displaystyle a{x}^2+bx+c}$  の因数分解

${\displaystyle a{x}^2+bx+c=\left(px+q\right)\left(rx+s\right)}$ 

のように因数分解できたとすると

${\displaystyle \left(px+q\right)\left(rx+s\right)}$

${\displaystyle =pr{x}^2+\left(ps+qr\right)x+qs}$

となり，係数を比較すると

${\displaystyle a=pr}$ ，${\displaystyle b=ps+qr}$ ，${\displaystyle c=qs}$ 

となる．

すなわち，因数分解を行うには，このような関係が成り立つ整数の組合せ${\displaystyle \left(p,q,r,s\right)}$ を求めればよい．

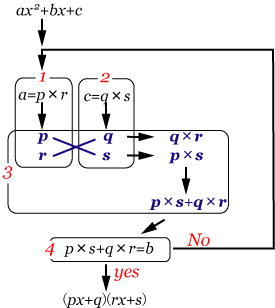
以下にその求める手順を示す．

1. ${\displaystyle x^2}$  の係数 ${\displaystyle a}$において${\displaystyle a=pr}$ となる整数${\displaystyle p}$ ，${\displaystyle r}$ の組合せ${\displaystyle \left(q,r\right)}$  を求める．

2. ${\displaystyle c}$において${\displaystyle c=qs}$ となる整数${\displaystyle q}$ ，${\displaystyle s}$ の組合せ${\displaystyle \left(q,s\right)}$  を求める．

3. 定数 ${\displaystyle c}$において${\displaystyle c=qs}$ となる整数${\displaystyle q}$ ，${\displaystyle s}$ の組合せ${\displaystyle \left(q,s\right)}$  を求める．

4. (1)，(2)で求めた組合せの中から1つずつ選び ${\displaystyle p\times s+q\times r}$  を計算する．

5. ${\displaystyle p\times s+q\times r=b}$  とならなければ(1)，(2)，(3) を${\displaystyle p\times s+q\times r=b}$  になるまで繰り返す（すなわち，${\displaystyle p}$ ，${\displaystyle q}$ ，${\displaystyle r}$ ，${\displaystyle s}$  の組合せを変える）．

6. ${\displaystyle p\times s+q\times r=b}$  が得られれば，求める因数分解の答は$\left(px+q\right)\left(rx+s\right)$  である．

青字の部分は実際に紙に書いて見るとよい．

■具体例

1. ${\displaystyle 6x^2-x-15}$  を因数分解する．
   ${\displaystyle x^2}$  の係数 ${\displaystyle 6}$において${\displaystyle 6=pr}$ となる整数${\displaystyle p}$ ，${\displaystyle r}$の組合せ${\displaystyle \left(q,r\right)}$  を求める．
   ${\displaystyle \left(p,r\right)=\left(1,6\right),\left(2,3\right),\left(3,2\right),\left(6,1\right)}$

2. 定数 ${\displaystyle 15}$において${\displaystyle 15=qs}$ となる整数${\displaystyle q}$ ，${\displaystyle s}$の組合せ${\displaystyle \left(q,s\right)}$  を求める．

   ${\displaystyle \left(q,s\right)=}$${\displaystyle \left(1,-15\right),}$${\displaystyle \left(3,-5\right),}$${\displaystyle \left(5,-3\right),}$${\displaystyle \left(15,-1\right),}$${\displaystyle \left(-1,15\right),}$${\displaystyle \left(-3,5\right),}$${\displaystyle \left(-5,3\right),}$${\displaystyle \left(-5,1\right)}$

3. $\left(1,6\right)$ と $\left(1,-15\right)$ の組み合わせ

   ${\displaystyle \begin{array}{lllll}1\hfill & {}_{\searrow }{}_{\nearrow }\hfill & 1\hfill & \to \hfill & 6\hfill \\ 6\hfill & {}^{\nearrow }{}^{\searrow }\hfill & -15\hfill & \to \hfill & -15\hfill \\ \hfill & \hfill & \hfill & \hfill & -9\hfill \end{array}}$

   $b=-1$ となっていないので，次の組み合わせを試す．

4. $\left(1,6\right)$ と $\left(3,-5\right)$ の組み合わせ

   ${\displaystyle \begin{array}{lllll}1\hfill & {}_{\searrow }{}_{\nearrow }\hfill & 3\hfill & \to \hfill & 18\hfill \\ 6\hfill & {}^{\nearrow }{}^{\searrow }\hfill & -5\hfill & \to \hfill & -5\hfill \\ \hfill & \hfill & \hfill & \hfill & 13\hfill \end{array}}$

   $b=-1$ となっていないので，次の組み合わせを試す．

5. $\left(2,3\right)$ と $\left(3,-5\right)$ の組み合わせ

   ${\displaystyle \begin{array}{lllll}2\hfill & {}_{\searrow }{}_{\nearrow }\hfill & 3\hfill & \to \hfill & 9\hfill \\ 3\hfill & {}^{\nearrow }{}^{\searrow }\hfill & -5\hfill & \to \hfill & -10\hfill \\ \hfill & \hfill & \hfill & \hfill & \mathbf{-}\mathbf{1}\hfill \end{array}}$

   $b=-1$ となり，因数分解ができる．

6. ${\displaystyle 6x^2-x-15=\left(2x+3\right)\left(3x-5\right)}$

 

ホーム>>カテゴリー別分類>>数と式>>整式：たすきがけ手法による因数分解の手順

最終更新日： 2024年9月19日