演習問題
■媒介変数表示における導関数媒介変数(パラメータ)表示された関数 x=√t−1−2 , y=t3−5 について導関数 dydx を t の式で表し,点 P(−1,3) における接線方程式を求めよ.
■陰関数の接線の方程式
■陰関数の接線の方程式
■3次関数のグラフの式を求める問題
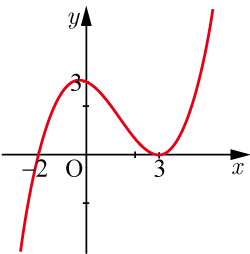
図は x 軸と点 (−2,0) で交わり,点 (3,0) で接し,y 切片が 3 の3次関数のグラフである.グラフを表す3次関数の式を求めよ.
媒介変数(パラメータ)表示された関数 x=√t−1−2 , y=t3−5 について導関数 dydx を t の式で表し,点 P(−1,3) における接線方程式を求めよ.

図は x 軸と点 (−2,0) で交わり,点 (3,0) で接し,y 切片が 3 の3次関数のグラフである.グラフを表す3次関数の式を求めよ.